こんにちは、小郷です。閲覧数のために挑発的なタイトルでイキりました(正直)。
さて、このページに辿り着いている方であれば、データ分析とかデータドリブン経営というような言葉を耳にしてきたことでしょう。ただ、一言でデータ分析と言っても、目的とやり方が色々あって「どれ使えばいいの?何ができるの?」という疑問を持たれる方も多いのではないかと思います。
本記事ではデータ分析の目的に応じた手法の使い分けや、それに付随した統計学の基本についてご紹介したいと思います。途中で出てくるいくつかの単語については、こちらの記事で一部を紹介しているので、ご興味あれば見てやってください。
全てを見たい?それとも予想をしたい?
データ分析を行う際は、まずは目標の設定をしましょう。「最終的に何が分かればいいのか」という事の設定ですね。
日常の中でも聞いた事があるであろう統計調査を、以下のグループに分けてみました。性質に応じて明確な差があるのですが、どんな差であるかを考えてみてください。
Aグループ
- 人口動態統計
- 企業におけるバランスシートの作成
- 学生の成績の集計
Bグループ
- 選挙開票速報
- 視聴率の算出
- アンケートによる市場調査
Aグループの分析は、観測対象のすべてのデータが得られ、全体あるいは個々の状態を正確に把握したいケースです。現状を把握し、問題があれば個別のデータにアクセスして改善案を考えることもあります。
それに対してBグループの分析は、得られる情報が限られているものの、その少ない情報から全体の傾向を予測したいケースです。全数を調査することが現実的に難しい場合でも、現状の傾向を把握して、施策に繋げたい時に用います。
統計学の用語では、Aグループの分析は記述統計と呼ばれ、Bグループの分析は推測統計と呼ばれます。それぞれについて見ていきましょう。
記述統計
この統計では、集めたデータの全体を要約したり、その特徴や傾向を示すことを目的とします。その特徴を記述するためには、統計量を使用します。記述統計においては、原則として観測対象のすべてのデータが必要です。(理論上は)全てのデータが集まってくる、学生のテストの平均値を出す、企業の売上を管理するというようなケースの集計に向いています。
統計量には以下のようなものがあります。
- 平均値(mean): 全てのデータの値を足し合わせ、データ数で割った値。
- 中央値(median): データを順番に並べたときに、真ん中にある値。
- 最頻値(mode): データの中で、最も高い頻度で出現する値。
- 最小値(minimum): データの中で最小の値。
- 最大値(maximum):データの中で最大の値。
以下も覚えておくと良いでしょう。
- 第一四分位数(1st quartile): データを小さい順に並べたときに、下位25%となるデータの分割点。
- 第三四分位数(3rd quartile): データを小さい順に並べたときに、下位75%となるデータの分割点。
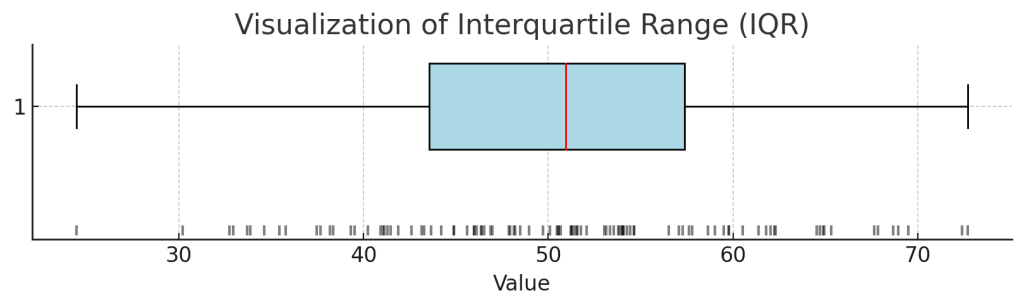
- 四分位範囲(IQR): データを順番に並べたときに、中央50%のデータの範囲。第一四分位数と第三四分位数の間に入るデータの範囲を指す。
文章だけだとちょっとわかりづらいので、Pythonに図を書かせてみます。いわゆる箱ひげ図と呼ばれるもので、左側のバーが最小値、右側のバーが最大値を表しています。四角部分の左側の境界が第一四分位数、右側の境界が第三四分位数を表し、赤いラインは中央値です。グラフ下部の黒く小さいバーが、個々のデータですね。
import matplotlib.pyplot as plt
import numpy as np
# 仮のデータセットを生成
np.random.seed(0)
data = np.random.normal(loc=50, scale=10, size=100)
# 四分位数を計算
q1, q3 = np.percentile(data, [25, 75])
iqr = q3 - q1
# 四分位範囲の可視化
plt.figure(figsize=(10, 2))
plt.title("Visualization of Interquartile Range (IQR)")
plt.xlabel("Value")
plt.yticks([]) # Hide Y-axis ticks
# Plot data points
plt.scatter(data, np.zeros_like(data), alpha=0.5, marker='|', color='black')
# Box for the interquartile range
plt.boxplot(data, vert=False, widths=0.7, patch_artist=True,
boxprops=dict(facecolor="lightblue", color="black"),
medianprops=dict(color="red"),
whiskerprops=dict(color="black"),
capprops=dict(color="black"),
flierprops=dict(marker='o', markerfacecolor='black', markersize=5, linestyle='none'))
plt.show()
ただ、国家機関の調査や、学校の単一学年内における小規模の調査でもない限り、現実的に全数を集めることは難しいです。システムからデータが綺麗に取れるようなケースでは、記述統計が向くでしょう。
取得できるデータが全数でない場合に活用するのが、推測統計です。推測統計を用いると、手に入る範囲のデータを使って全体の傾向を予測できます。
推測統計
唐突ですが、皆様は総選挙には行っていますでしょうか。アイドルやキャラクターの人気投票ではなく、政治家を国政に送り込むか無職にするかを決める方の選挙です。
選挙当日は、夜の20:00に投票が締め切られるのと同時に、各テレビ局の選挙特番が始まる光景が記憶にあると思います。そして、番組開始と同時に〇〇党の議席が何席確定、というような発表がなされると思います。
20:00に開封が開始して、20:00の時点で議席数がわかってしまうなんて、変ですよね。投票先を事前に監視あるいは指示するような仕組みでもあるのか、あるいは選挙など無駄で全て票が事前に決まっているのかと陰謀論チックなことを思ってしまうかもしれませんが、それをやってしまうと独裁国家が誕生します。
しかし、投票先を事前に知る仕組みがある、というのは間違っていません。出口調査という言葉を聞いたことはあるでしょうか。投票した人にランダムに声をかけて、どの党に投票したのかをヒアリングすることです。この出口調査の結果を用いて議席数を事前に予測する際に、推測統計が使われています。
さて、ここから先は正規分布などの統計知識が必要になってきます。まだの方は、前回の記事からご確認ください(ダイマ)。
母集団と標本
推測統計の説明をするにあたって、大切な概念が存在します。
- 母集団: 数が既知あるいは未知のデータの全体
- 標本: 母集団の中から抽出したデータの集団
総選挙では、母集団が全ての投票の結果、標本が出口調査の結果にあたります。実際のデータとしては母集団が存在しているが、全数把握は難しいので標本を使って母集団の特性を推測する、という工程を推測統計と呼びます。
標本抽出
先ほど、出口調査のサンプルはランダムに選ばれることに触れました。どうしてランダム性が必要なのでしょうか。これは、できる限りランダムにサンプルを集めることは、母集団から標本が選ばれる可能性を平等にするためです。平等なサンプリングをすることで、母集団を正当に評価できるようになります。
例えば出口調査の対象を高齢男性のみ、あるいは若い女性のみ、というように絞ってしまうと、母集団の中の一部だけを代表する標本を集めてしまうので、母集団全ての特徴を掴む根拠として適切とは言えません。このような偏りを避けるため、対象はランダムに選ぶ必要があります。
ランダムサンプリングの方法には、以下のようなものがあります。
- 単純無作為抽出法: 全母集団から等しい確率で無作為に個体を選ぶ方法
- 系統抽出: リスト化された母集団から一定の間隔でサンプリングする方法
- 層化多段抽出法: 母集団をいくつかの層(サブグループ)に分け、その各層からランダムにサンプリングする方法
標本の統計量
ここまでで、おそらく均等であろう標本が集まったものとします。標本の特徴を集計して母集団の特徴を推測するには、いくつかのプロセスがあります。以降の説明で出口調査を例にすると、概念的に難しくなってしまうので、身長を例にすることとします。
標本平均は、集まった標本の計測値の平均です。集めたサンプルの値を足して、サンプル数で割って求めることができます。最も直感的にわかりやすい文脈では、「渋谷の街をゆく成人男性にランダムに声をかけて、身長の値をヒアリングする。この値の平均を標本平均とする」というものですね。
出口調査でも同じことが言えます。概念を理解するために、各有権者が投票した候補者に1、それ以外は0という値を与えます。日本の選挙は1人1票になっているはずなので、無効票や無記名投票をしない限り、1000人の投票結果を集めた場合の投票数の合計は1000になります。
| 候補者A | 候補者B | 候補者C | 候補者D | |
| 有権者1 | 1 | 0 | 0 | 0 |
| 有権者2 | 1 | 0 | 0 | 0 |
| 有権者3 | 0 | 1 | 0 | 0 |
| 有権者4 | 0 | 0 | 1 | 0 |
| ….. | ….. | ….. | ….. | ….. |
| 得票合計 | 600 | 250 | 100 | 50 |
この表の縦方向を合計すると、候補者別の得票数を算出することができます。また、各候補者の得票数を投票数で割ることで、得票率を求められます。ここで得られた得票率は、各有権者が各投票者に投票した票数の平均と捉えることもできます。つまり、1000人の有権者は平均して、候補者Aに0.6票を投じたと見なすことができます。これで、候補者Aの得票率の標本平均を得ることができました。
標本分散と不偏分散
まずは平均(Xバー)とデータポイントごとの値(Xi)とデータ数(n)がわかっているので、標本分散まで一気に求めてしまいましょう。
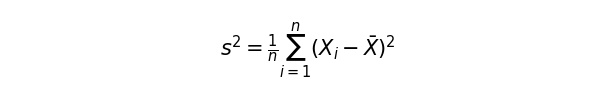
この標本分散から、不偏分散を計算します。特に標本サイズが小さい時、母集団の性質を正確に表せない場合があります。標本分散の期待値は、母分散の期待値はよりも小さくなる傾向にあります。そのため、データの自由度(n – 1)で補正をかけます。
分母のnをn – 1に置き換えてあげることで、不偏分散を求めることができます。前回の記事で求めた分散の式に一致しました。このあたりの証明は結構長くなってしまうので、気になる方は調べてみてください。
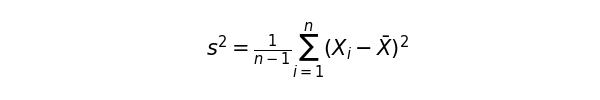
pythonに計算させると、不偏分散は0.2402になります。
import numpy as np
# 不偏分散を直接計算する
# X_i の値は 1 または 0 です(1 = 候補者に投票, 0 = 投票していない)
# このケースでは、600票が候補者に行き、400票が行っていない
votes = np.array([1]*600 + [0]*400)
sample_mean = votes.mean()
# 不偏分散 s^2 の計算
unbiased_variance = ((votes - sample_mean) ** 2).sum() / (n - 1)
次に標準誤差を求めます。この指標は、標本から得られる推定量(標本平均)のばらつきを表すものです。標本平均がどれほど母集団の平均からずれやすいかという指標です。これが小さいほど、母集団とのズレは小さいとみなします。不偏分散の平方根をnの平方根で割ります。
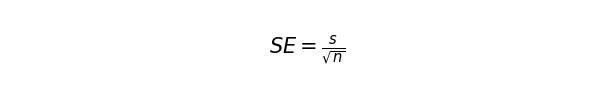
先のコードの続きに以下を書き加えて、標準誤差を計算しましょう。その値は0.0155となります。
# 標準誤差の計算
std_error_unbiased = np.sqrt(unbiased_variance / n)
中々に複雑ですが、そろそろ母集団平均を推定できます。ここでは信頼区間を計算します。よく使われる指標は95%信頼区間です。意味合いとしては、「この区間になら9割5分、母集団の平均値が含まれるだろう」という区間です。次の式で求められます。
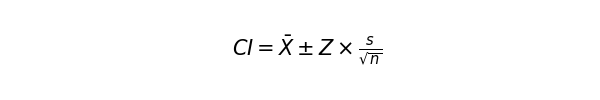
Zは信頼区間に応じたZスコア標準正規分布(平均0, 標準偏差1)に基づいて求められた値です。検索すると、以下のような標準正規分布表が出てきます。
https://unit.aist.go.jp/mcml/rg-orgp/uncertainty_lecture/normsdist.html
95%のデータが入る、つまり両端2.5%ずつは含まない範囲を求めたいので、表から0.025を探します。最も近い値は「0.024998」ですね。表の左側の値と上の値を組み合わせて、95%信頼区間におけるZスコアは1.96と定義することができます。「標準正規分布において、95%の値が±1.96の範囲に入る」という意味ですね。このZスコアに対して標本誤差を掛けたものを、標本平均にプラスまたはマイナスすると、「母集団を調べたわけじゃないけど、母集団平均値は大体こんなもんだろう」という値を求めることができます。
Zスコアはscipyから取得できます。それを元に、95%信頼区間を計算してみましょう。結果は56.96%から63.04%になります。過半数の票は取れているので、当選確実と言っていいでしょう。
ちなみに0.975としているのは、0.025~0.975の間に95%のデータが入るという意味です。ちょっとややこしいですね。95を引数にできたら直感的にわかりやすいんですが。
from scipy.stats import norm
z_score = norm.ppf(0.975)
ci_lower_unbiased = sample_mean - z_score * std_error_unbiased
ci_upper_unbiased = sample_mean + z_score * std_error_unbiased
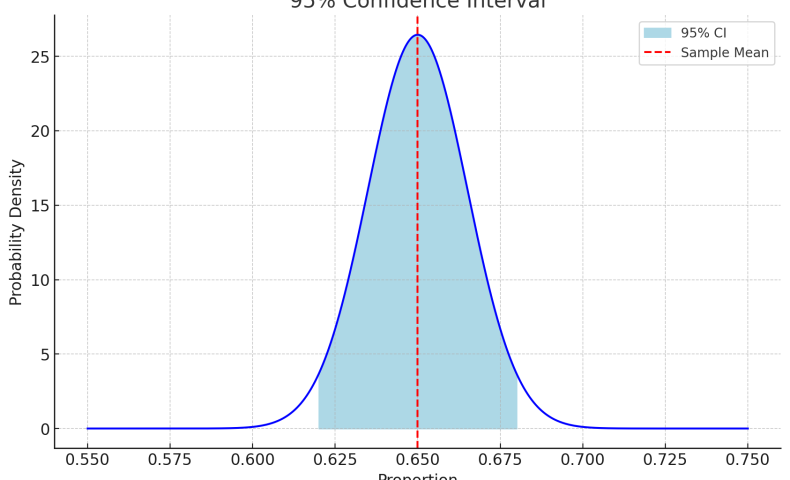
以下は視覚的に、95%の値が入る範囲を示したものです。
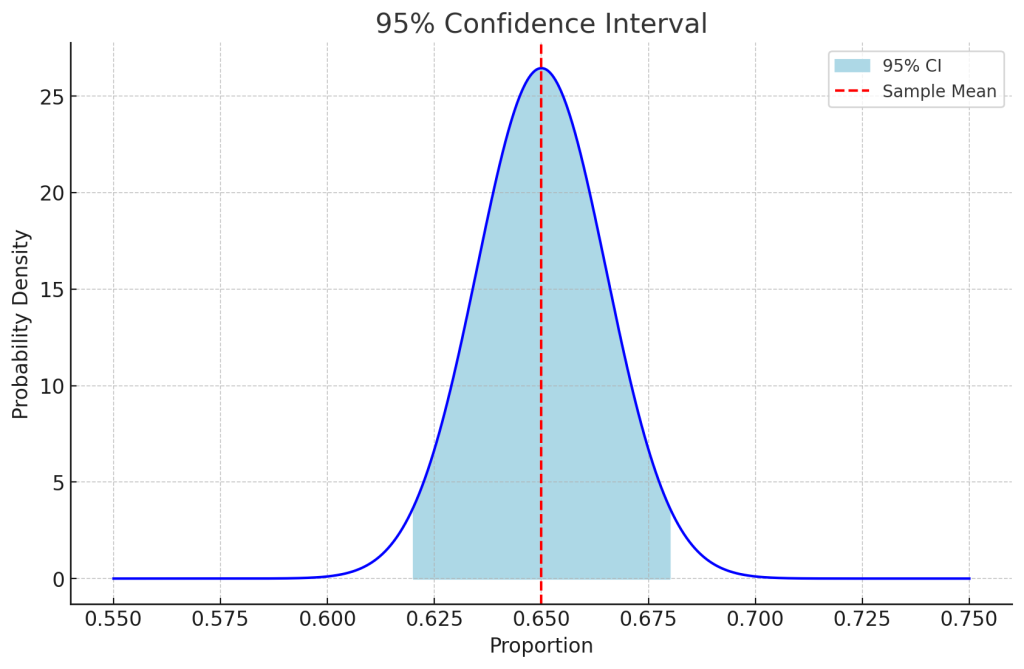
推定の制度を高める、例えば99%にした場合、推定は正確になるものの、標準誤差×Zスコアの絶対値は大きくなります。逆に、推定の制度を下げると、標準誤差×Zスコアの絶対値は小さくなります。また、分散が大きければ信頼区間の範囲は大きくなります。
これで、標本データから母集団を推定できる仕組みがなんとなく分かったかと思います。
二項分布による近似
選挙の投票のように、した/しないという2つ結果しかない試行(ベルヌーイ試行)を複数回行った時、ある事象が何回起こるかの確率分布を二項分布と呼びます。ここまで真面目に読んでいただいた方には申し訳ないですが、二項分布は試行回数が大きい場合に正規近似ができることから、先のような面倒臭い計算をしなくても簡単に信頼区間を求めることができます。これをド・モアブル=ラプラスの定理と呼びます。美少女人形がバトルする某作品でラプラスの魔を通ったオタクの琴線に触れる単語ですね。
細かい証明は省きますが、標準誤差は以下で計算できます。ここで、p hatは計測値を指します。今回のケースでは0.6ですね。

標準誤差さえ求めてしまえば、信頼区間は簡単に求めることができます。56.96から63.04となり、先に頑張って求めた値と近い値になりました。
from scipy.stats import norm
import numpy as np
# パラメータ設定
n = 1000 # サンプルサイズ
x = 600 # 投票数
p_hat = x / n # 標本平均
# 1. 標本平均から不偏分散を計算する方法
std_error = np.sqrt(p_hat * (1 - p_hat) / n) # 標準誤差
z_score = norm.ppf(0.975) # Zスコア (95%信頼区間)
# 信頼区間
ci_lower = p_hat - z_score * std_error
ci_upper = p_hat + z_score * std_error
最後に
全数比較か、それともサンプリングからの推定か。それによって取れる手法が異なることを説明しました。出てきた集計値の集計元のデータが何であるか、という点はしっかり把握しておく必要があります。
当然ですが、推定には限界があります。
- サンプルサイズ: サンプルサイズが小さいほど、母集団の特性を正確に反映していない可能性が高く、ばらつきが大きくなります。
- バイアス: アンケート調査などでは、「デフォルト」や「中心化傾向」など、複数の心理学的バイアスが働くとされています。これらはデータに対して誤差を与える要因です。また、当然ですがサンプルに偏りが生じる可能性は排除不可能です。
- あくまで確率: 推定はあくまで確率を示すものであるため、100%正しくはなりません。つまり、95%信頼区間で求めた範囲から、5%くらいの確率で外れることがあります。
なので、全幅の信頼を置いていい値ではありません。そのあたりは最近話題の生成AIとも一緒ですね。膨大な学習データ(標本)から次に来る単語を推論しているにすぎないので、それっぽい内容を返してきているイメージです。あえてバイアスかけて、例えばキャラクターを演じさせるような使い方もできたりするんですが。
今回は以上です。日常の中にもデータサイエンスが存在していることをちょっとでも実感していただけたなら幸いです。
付録: サムネ画像を作ったコード
import matplotlib.pyplot as plt
import numpy as np
# 95%信頼区間のデータ準備
mean = 0.65 # 標本平均
ci_lower, ci_upper = 0.62, 0.68 # 95%信頼区間の下限と上限
# 標準正規分布のプロット
x = np.linspace(0.55, 0.75, 1000)
y = norm.pdf(x, mean, se)
plt.plot(x, y, color="blue")
# 信頼区間のシェーディング
plt.fill_between(x, y, where=(x >= ci_lower) & (x <= ci_upper), color="lightblue", label="95% CI")
# 標本平均の線
plt.axvline(x=mean, color="red", linestyle="--", label="Sample Mean")
# 装飾
plt.title("95% Confidence Interval")
plt.xlabel("Proportion")
plt.ylabel("Probability Density")
plt.legend()
plt.show()