こんにちは、小郷です。
「IQ」という言葉について、日常的にはテレビ番組のタイトルや、芸能人の〇〇はIQが148以上ある天才だ、という文脈で耳にすることがあると思います。また、ネットのごく一部の界隈で、境界知能(IQ85~70)という言葉が否定的な文脈で使われているのを聞いたかもしれません(本来は支援が受けられない人々を拾い上げるための言葉です)。
本記事ではIQ148やIQ85がそれぞれ何を意味するかを解説し、統計学の理解を深めていただくことを目的としています。
IQとはそもそも何か
Intelligence Quotient(知能指数)の略で、知能検査の結果の表示方式の一つです。英国人の平均を100としたときに、相対的にどの程度のスコアを取れているかで算出します。
IQが高いということは、IQテストの点数が高いという意味です(kizm構文)。IQは現代の先進国における知的労働にどの程度適応的かを表す指標であり、人間の価値の全てを決定づける値ではなく、たった一つの側面を評価する指標にすぎないことは明記しておきます。
ばらつきの異なる3つのテスト
上位2%のIQを持つ人が入会資格を得る「MENSA」というグループの名前を聞いたことがあるかも知れません。上位2%のIQとは具体的な数値で幾つなの?と調べてみると、以下の三つが出てくると思います。
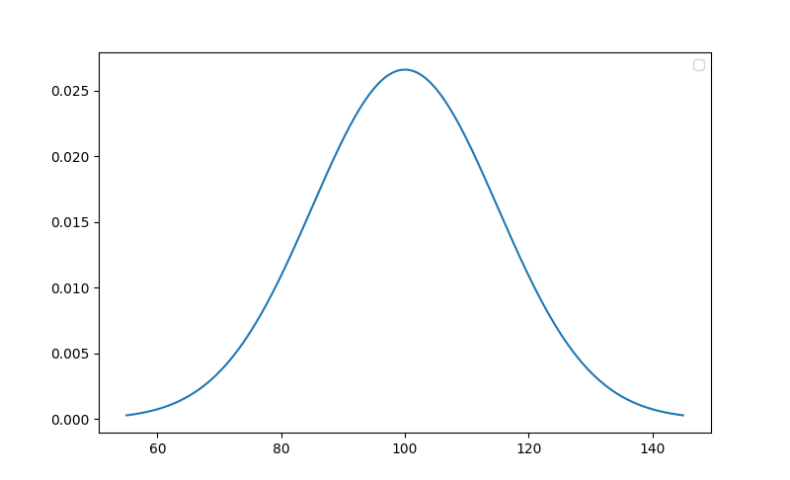
- 130(ウェクスラー式): アイキャッチ画像のグラフはこちらに該当します。
- 132(ビネー式)
- 148(キャッテル式)
130以上で上位2%なら、148はもっと上じゃないの?あるいは、148以上が上位2%なら、130は基準を満たさないんじゃないの?と思うかも知れませんが、出し方が違うだけで130/132/148は全て上位2%の基準値です。
どういう事かを理解するためには、統計学の知識が必要です。今は「IQの値だけでは意味がなく、どの種類のテストを受けたかセットじゃないと評価できない」という事をなんとなく頭の片隅に置いておいてください。
それぞれのテストで計測基準や計測項目が違ったりしますが、ここでは一旦無視して、数字にだけ着目して話を進めます。
ばらつき
例えば、以下のシチュエーションを想像してみましょう。
- スーパーで買ってきた100個のジャガイモの重さを1つずつ計測する
- 100人に同じテストを受けさせて、1人1人の得点を記録する
経験則として、ジャガイモの重さやテストの点数が全てのケースで同じということはなく、それぞれで異なった値になりますよね。これをばらつきと呼びます。
IQテストも同じです。人それぞれスコアは違いますよね。そして、多くのサンプルを集めると、100点の人がn人、101点の人がm人と、スコアを横軸に、人数を縦軸にしたグラフを作ることができます(ヒストグラムと言います)。
手元にデータがあるわけではないですが、先人の研究や調査により、80, 100, 120,それぞれのIQスコアを持つ人数は同じではなく、100を中心に人数が大きく、高低両端のスコアになるほど人数が少なくなることがわかっています。
身長を例にしてみると感覚的にわかりやすいと思いますが、極端に背が高い人や、逆に極端に背が低い人の数は、平均的な身長の人よりも見かける機会が少ないですよね。IQにも同じことが言えます。
身長や知能は多数の遺伝子や、栄養状態などの後天的な因子が関係すると言われています。これらの要素ひとつひとつを変数と考えることができ、個々の影響が小さい多くの変数が合わさると、その結果は平均に近づくという現象が存在がわかっています。そして、この傾向がある値を数多く集めると、平均的な値を持つサンプルの数が多くて、極端な値を持つサンプルの数は少なくなります。このような値の分布を正規分布と呼び、統計学においては重要な概念です。
確率分布
数学的に捉えやすい例で考えてみましょう。2つのサイコロを振り、その出た目の合計を計測します。
ちなみに、今回の例に挙げたサイコロの目の合計値のような、試行の結果によって値が定まる変数を確率変数と呼びます。IQや身長も確率変数と言えます。
これを10000回繰り返した際に、それぞれの合計値が何回出現したか(度数と呼びます)をヒストグラムで表します。実際に計測すると疲れるので、pythonに処理させることにしました。コードで書くと以下です。
import matplotlib.pyplot as plt
import random
# サイコロを振る回数
n_rolls = 10000
# サイコロの出目の合計を記録するリスト
totals = []
# サイコロを10000回振る
for _ in range(n_rolls):
die1 = random.randint(1, 6)
die2 = random.randint(1, 6)
totals.append(die1 + die2)
# ヒストグラムを作成する
plt.hist(totals, bins=range(2, 14), edgecolor='black', align='left')
plt.title('Histogram of the Sum of Two Dice')
plt.xlabel('Sum')
plt.ylabel('Frequency')
plt.grid(True)
plt.show()
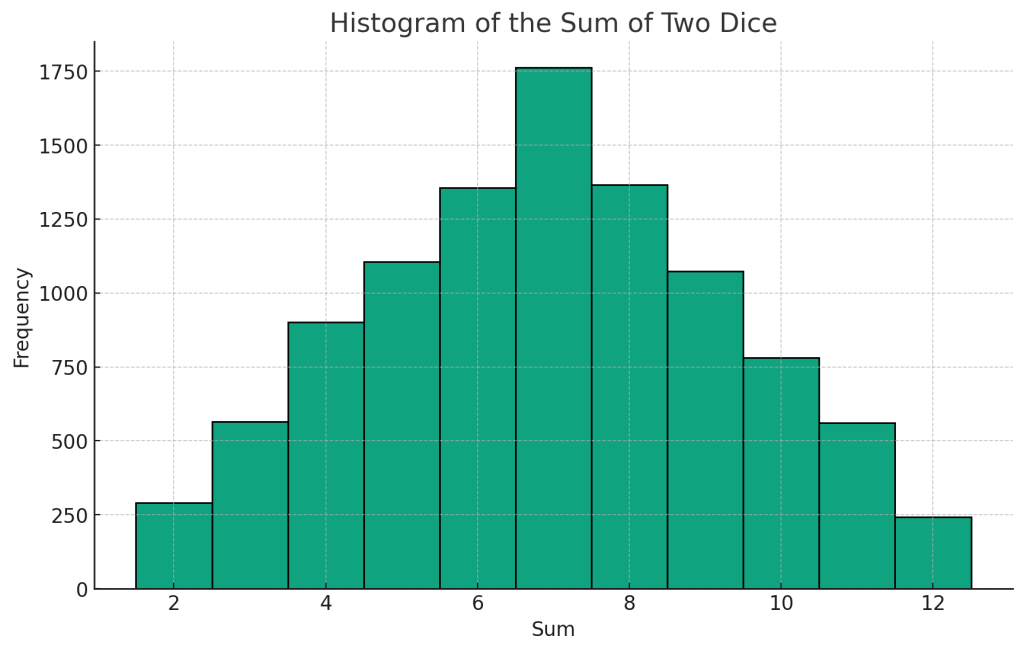
サイコロの目の組み合わせを考えると、7となる組み合わせが最も多くなります。[1+6][2+5][3+4][4+3][5+2][6+1]という6パターンです。次点は6と8ですね。[1+5][2+4][3+3][4+2][5+1]と、[2+6][3+5][4+4][5+3][6+2]でそれぞれ5パターンです。最も少ないのは2と12で、[1+1]と[6+6]のパターンしかありえません。
それぞれの合計値がどの程度出やすいかは、数学的に計算する事ができます。サイコロの目の出方は36通りですから、合計値のパターン数を36で割るとそれぞれの出る確率が求められます。7だと、1/6の確率で出る事がわかります。
確率変数が7という値をとる確率は、数学的には1/6ということわかりました。また、それぞれの値もどの確率で出るかを求めることができます。そうして個々の値とその確率を対応させたものを、確率分布あるいは分布と呼びます。
2つのサイコロの目の合計は、取りうる値が11個に決められています。このような確率分布を、離散型確率分布と呼びます。その一方で、現実的には整数に丸められて語られるものの実態としては無限に値を取りうる、身長やIQが取る分布のことを連続確率分布と呼びます。
連続確率分布「っぽい」グラフを描かせてみましょう。どうしても人間が評価するにあたっては、ある程度の単位で区切ってグラフを作らなければいけませんが(階級と呼びます)、現実的な観測値は連続している事が多いです。こちらも実際に計測するのは骨が折れるので、例の如くPythonにイメージ図を描かせてみます。
import numpy as np
import matplotlib.pyplot as plt
# 正規分布に従うランダムデータを生成
data = np.random.normal(0, 1, 1000)
# ヒストグラムを作成
plt.hist(data, bins=100, edgecolor='black')
plt.title('Normal Distribution Histogram (Finer Bins)')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.grid(True)
plt.show()
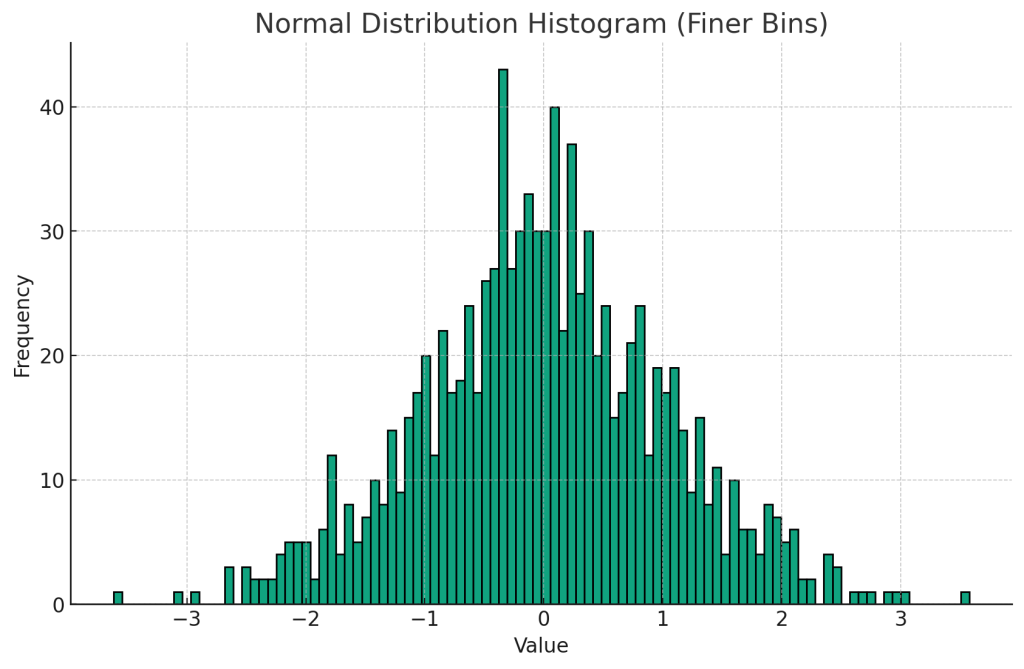
このグラフの区間をさらに分割していくと、サムネイル画像のような曲線になります。
平均・分散・標準偏差
「で、結局、IQの上位2%ってどう決まるの?」という本題に戻ろうと思います。
IQのスコアと、そのスコアをもつ人の数は、正規分布に従うと考えられていることを説明しました。この正規分布のグラフの形を決めるパラメータとして、平均と標準偏差という概念が存在します。
平均はイメージしやすいですよね。全ての観測値を足し合わせて、その数で割れば良いのです。確率変数をX、Xが実際にとった観測値を X1, X2 …とすると、平均値は以下の式で表すことができます。
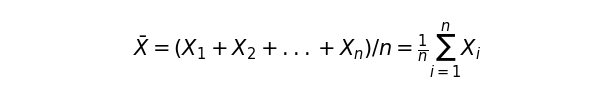
平均が定まると、グラフの位置を決定する事ができます。IQは100に固定しているため、この概念は身長の分布を男女間比較するとわかりやすいと思います。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# 男性の平均身長と標準偏差
male_mean = 170
male_std = 7
# 女性の平均身長と標準偏差
female_mean = 158
female_std = 6
# 身長の範囲を設定
height_range = np.linspace(130, 210, 1000)
# 正規分布の確率密度関数(PDF)を計算
male_pdf = norm.pdf(height_range, male_mean, male_std)
female_pdf = norm.pdf(height_range, female_mean, female_std)
# グラフをプロット
plt.figure(figsize=(10, 6))
plt.plot(height_range, male_pdf, label='Male Height Distribution', color='blue')
plt.plot(height_range, female_pdf, label='Female Height Distribution', color='pink')
plt.xlabel('Height (cm)')
plt.ylabel('Probability Density')
plt.title('Comparison of Male and Female Height Distributions')
plt.legend()
plt.grid(True)
plt.show()
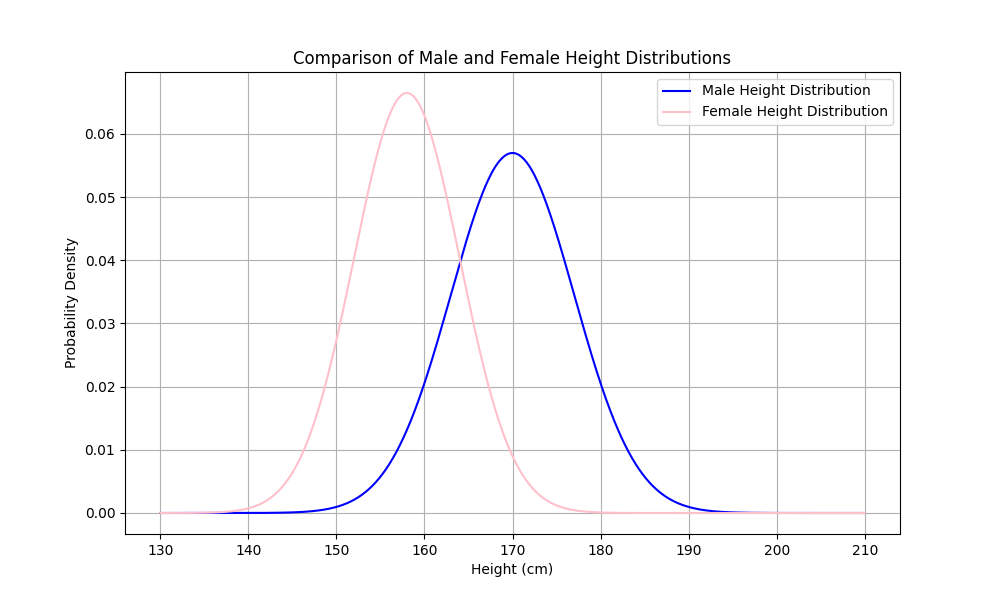
成人男性の平均身長を170cm、標準偏差を7cmと仮定しました。また、成人女性の平均身長を158cm、標準偏差を6cmと仮定しています。感覚的にも女性の方が平均的に身長が低いというのはわかると思いますが、実際に分布を書いてみると、男性の身長分布が女性の身長分布に比べて右側(より高い身長)に位置していることが視覚的に確認できます。
さて、さらっと出てきた標準偏差という言葉ですが、これはデータのばらつきを表す指標です。標準偏差は、グラフの山の高さと、横の広がりを決めます。上記のグラフでも、山の高さが少しだけ違う事がわかると思います。
標準偏差を求めるために、まずはそれぞれの値と平均値との差(偏差と呼びます)を求めてみましょう。これは簡単に求める事ができます。
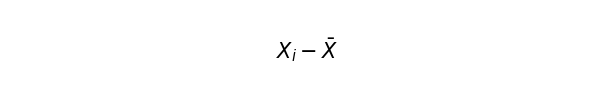
平均より大きい値に対する偏差は正の値で、平均より小さい値に対する偏差は負の値になります。実は偏差の合計は0になってしまうので、このままでは全体の散らばりを表す指標としては使えません。そこで、偏差を2乗して合計した指標を使うのが一般的です。これを偏差平方和(SSD)と呼びます。
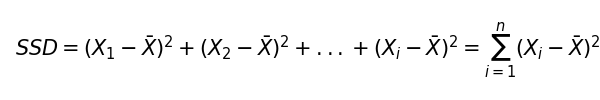
ただこのままでも、データの数が多ければ多いほど、偏差平方和が大きくなってしまうことから、やはり全体のばらつきを表す指標としては相応しくありません。そこで、データ数で補正をかけます。これを分散と呼びます。
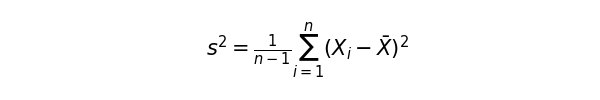
n – 1は、データの自由度と呼ばれます。平均値が定まっている時に、n – 1個のデータを決定すると、残り1つのデータは平均値に合わせて自ずと決まります。これが、自由度がn – 1であるということです。少しややこしい話なので、そういうものだと思っていただければ大丈夫です。
最後に、上記は2乗になっているため、計測したデータと単位を合わせる必要があります。分散の平方根を取ったものを標準偏差と呼びます。この値は性質上、個々のデータが平均から離れていれば離れているほど、大きい値を取ります。
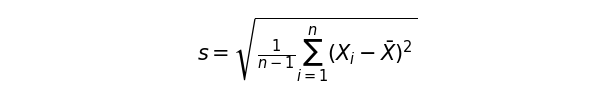
正規分布のグラフに、標準偏差を表すバーを引いてみましょう。
# IQ分布用にグラフを再設定
mean_iq = 100 # IQの平均
std_iq = 15 # IQの標準偏差
# IQの範囲を設定
iq_range = np.linspace(40, 160, 1000)
# IQ分布の確率密度関数(PDF)を計算
iq_pdf = norm.pdf(iq_range, mean_iq, std_iq)
# グラフを再プロット
plt.figure(figsize=(10, 6))
plt.plot(iq_range, iq_pdf, label='IQ Distribution', color='green')
# 平均、SD1、SD2の位置に線を引く
plt.axvline(x=mean_iq, color='grey', linestyle='--') # 平均値
plt.axvline(x=mean_iq - std_iq, color='blue', linestyle='--', label='SD1 (-)')
plt.axvline(x=mean_iq + std_iq, color='blue', linestyle='--', label='SD1 (+)')
plt.axvline(x=mean_iq - 2*std_iq, color='red', linestyle='--', label='SD2 (-)')
plt.axvline(x=mean_iq + 2*std_iq, color='red', linestyle='--', label='SD2 (+)')
plt.xlabel('IQ')
plt.ylabel('Probability Density')
plt.title('IQ Distribution with SD1 and SD2')
plt.xticks(np.arange(40, 161, 15))
plt.legend()
plt.grid(True)
plt.show()
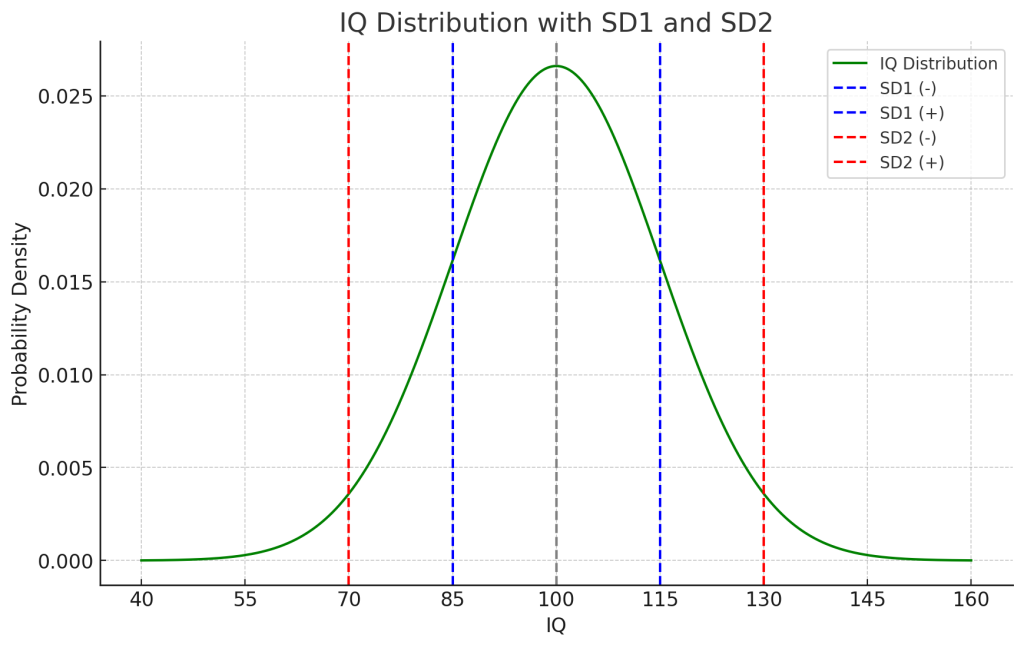
平均が100、標準偏差が15であるウェクスラー式IQテストの正規分布を表すグラフです。正規分布の面積は、合計すると1になります。そして、平均±標準偏差となる範囲に、68.2%のデータが入る性質があります。平均±2標準偏差となる範囲に、95.8%のデータが入ります。つまり、上位の2.1%と下位の2.1%は、平均±2標準偏差の位置することになり、MENSAの入会基準はここに設置されているわけですね。
IQの値はテストの名前が一緒にないと意味がないということ
さて、ようやく前提となる情報が揃いました。ここから、3種類のIQテストについて見ていきます。先ほど説明した通り、ウェクスラー式は平均が100、標準偏差が15のテストです。
対してビネー式は、平均が100というのは同じですが(IQテストではそうなるようにスコアが計算されます)、標準偏差が16になっています。これはテストの内容の違いによるもので、ばらつきがウェクスラー式よりも出やすくなっています。同様に、キャッテル式は標準偏差が24です。それぞれのグラフを書くと以下のようになります。
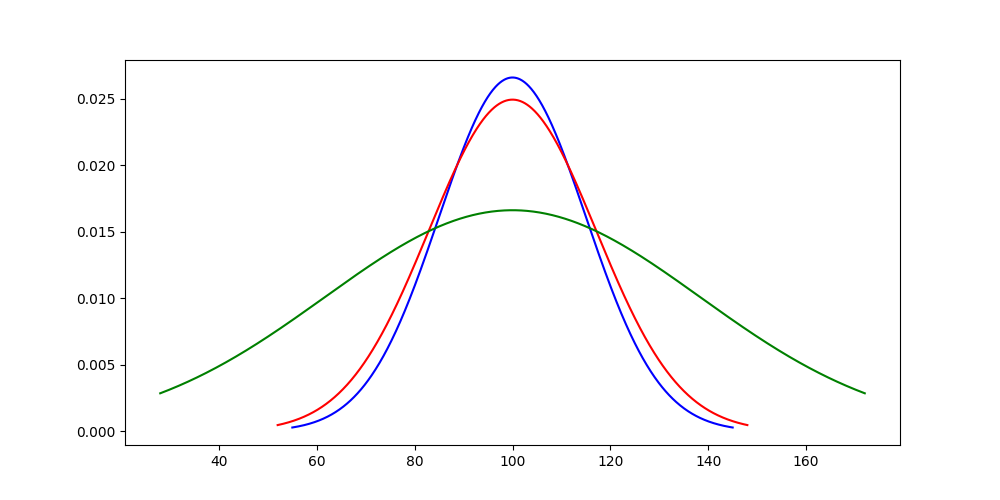
さて、冒頭では以下の2種類の文脈でIQが使われることがあると紹介しました。
- 芸能人の〇〇はIQが148以上ある天才
- 境界知能(IQ85~70)
おそらく前者は、標準偏差を24とした場合の右方SD2の値である148を値として示しているので、キャッテル式におけるスコアの話をしているのでしょう。後者は標準偏差を15とした場合の左方SD1以下の値を示しているので、ウェクスラー式におけるスコアの話をしているのでしょう。このあたりを理解せずにIQの話をすると、齟齬が発生してしまいますね。
前半で述べた、「IQの値だけでは意味がなく、どの種類のテストを受けたかセットじゃないと評価できない」という言葉の意味が、ここまでの解説でご理解いただけたかなと思います。
最後に
今回は日常に根ざした題材をもとに、統計学の基礎的な部分について触れました。本記事の内容が仕事につながるか、そこまでいかなくても日常における疑問を解決するような内容になっていれば幸いでございます。
ただし、現実のビッグデータは正規分布に従っていないことも多いのは事実です。次回以降の記事でこれ以外の分布や、それらの使い所をご紹介できれば良いかなと考えています。
とぅーびーこんてぃにゅーど