エクスチュア株式会社ブログ

RNNでsin曲線を予測

RNNとは

RNN(Recurrent Neural Network)とは、再帰型ニューラルネットワークの略で「ある時点の入力がそれ以降の出力に影響を与える」ニューラルネットワークのことです。
RNNでは過去の連続したデータから学習した結果を次の層の入力として再利用します。
※正確ではないのですが、まずはこのくらいの理解で大丈夫です。
得意分野は「機械翻訳, 言語認識, 文章生成」であり、それ以外でも「時系列をもつ音声/動画解析, 株価予測」などで応用されています。

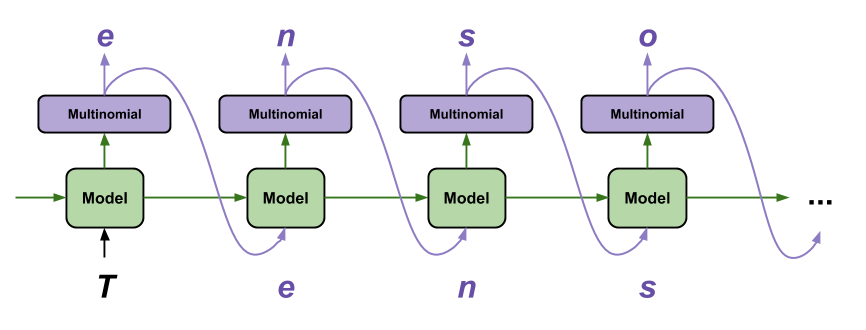
source: TensorFlow Text generation with an RNN | TensorFlow Core

RNNでsin曲線を予測

'''ライブラリの準備'''
import torch
import torch.nn as nn
from torch import optim
import torch.nn.functional as F
from torch.utils.data import DataLoader
from torch.utils.data import TensorDataset
import numpy as np
import matplotlib.pyplot as plt
'''GPUチェック'''
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print(device)

まずはいつも通りライブラリを用意し、GPU上で動いているかをチェックします。

'''訓練データ'''
x = np.linspace(0, 4*np.pi)
sin_x = np.sin(x) + np.random.normal(0, 0.3, len(x))
plt.plot(x, sin_x)
plt.xlabel('x')
plt.ylabel('sin(x)')
plt.show()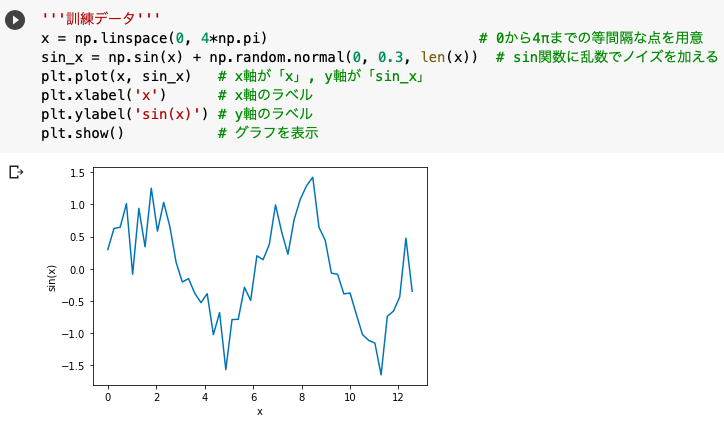

今回はsin波にノイズを与えたものを訓練用データとし、それをRNNが正しく形に再現(予測)できるかを検証していきます。
sin波にノイズを与えるために、正規分布に従う乱数を生成するnp.random.normal(平均, 標準偏差, 配列のサイズ)を使用しました。

'''ハイパーパラメータ'''
n_time = 10
n_sample = len(x) - n_time
'''データを格納する空の配列を準備'''
input_data = np.zeros((n_sample, n_time, 1))
correct_data = np.zeros((n_sample, 1))
'''前処理'''
for i in range(n_sample):
    input_data[i] = sin_x[i:i+n_time].reshape(-1, 1)
    correct_data[i] = [sin_x[i+n_time]]
input_data = torch.FloatTensor(input_data)
correct_data = torch.FloatTensor(correct_data)
'''バッチデータの準備'''
dataset = TensorDataset(input_data, correct_data)
train_loader = DataLoader(dataset, batch_size=8, shuffle=True)

◆ハイパーパラメータ
まずは何個の時系列データを1セットとするか(n_time)を決めます。
RNNは再帰的に処理を行うので過去データ(および出力結果)をまとめて扱う必要があり、そのまとめて扱うサイズをn_time=10で決めたのです。
今回はこの10個で1セットの移動を全データ(50個)に対して行いたいので、利用できるデータはn_sample=40個と決まります。
◆データを格納する空の配列を準備
利用できるデータが40個なので、正解値を格納する配列は[40, 1]と決まります。
ただ、入力値は10個のデータをもとに動くので配列のサイズは[40, 10, 1]でなければいけません。
◆前処理
前処理は利用する40個のデータ全てに対して行います。
まずsin_x[i]からsin_x[i+9]までの10個のデータを1つの入力(input_data[i])として配列へ格納し、その次のsin_[i+10]のデータを正解値としました。
この後の処理はtensor型で扱いたいのでtorch.FloatTensor(32bit小数のtensor型)へ変換します。
◆バッチデータの準備
入力と正解のtensor配列をTensorDatasetで1つのデータセットとしてまとめ、DataLoaderでバッチデータを用意しました。

'''モデルの定義'''
class RNN(nn.Module):
    def __init__(self):
        super(RNN, self).__init__()
        self.rnn = nn.RNN(1, 64, batch_first=True)
        self.fc = nn.Linear(64, 1)
    def forward(self, x):
        batch_size = x.size(0)
        x = x.to(device)
        x_rnn, hidden = self.rnn(x, None)
        x = self.fc(x_rnn[:, -1, :])
        return x
model = RNN().to(device)

pytorchにはデフォルトでRNNモジュールが用意されているので、今回はそれをそのまま利用します。
※nn.RNNにはデフォルトで「tanh」という活性化関数が組み込まれているので、明示的に活性化関数は示していません。
またRNNは1つの入力を連続的に行うので入力サイズは1、隠れ層の大きさは64、batch_first=Trueで設定しました。
※batch_firstは、ただnn.RNNの引数の順番を変更する役割なので特に気にしなくて大丈夫です。
そして全結合層は隠れ層のサイズ64を入力とし、予測したsin(x)の値を1つ返せば良いので出力のサイズは1となります。
次に、forward関数の中をみていきます。
x.size(0)で入力の行数(データの数)をbatch_sizeに設定し、x.to(device)すなわちx.to(‘cuda’)で学習の入力を全てGPUへ移行します。
そしてself.rnnではself.rnn(入力, 隠れ層の初期値)とする必要があり、その戻り値として一つは次の層への出力(x_rnn)、もう一つは現在の隠れ層の状態(hidden)を得ます。
また、x_rnn[:, -1, :]（10個の時系列ごとに出力されるデータの最後のものだけ）を全結合層に送りこむことで、最終的な計算結果（10個のデータを基にモデルが推測した次の値）を得ることができるというわけです。
今回はとてもシンプルな形で記述しましたが、本質的には以下のようになります。

まずコンストラクタ(def __init__)の部分で「入力の大きさ, 隠れ層の大きさ, 出力の大きさ, 層の数」を引数に設定します。
層の数(n_layers)と隠れ層の大きさ(hidden_size)は、後の関数(def init_hidden)でも利用するためにオブジェクト変数として「self」をつけて定義する必要があります。
※n_layersとhidden_sizeに「self」をつけ忘れると、”def __init__”の外で利用することができません。
勘の良い人はお気づきかと思いますが、上で利用した「None」は本質的には「torch.zeros(self.n_layers, batch_size, self.hidden_size)」を表しているのです。
※ただRNNを試したい方であればここまで理解していなくても問題ございません。

'''最適化手法の定義'''
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)
'''誤差(loss)を記録する空の配列を用意'''
record_loss_train = []

これまで評価方法はCrossEntropyLoss(交差エントロピー誤差)でしたが、今回は出力が1なのでMSELoss(平均二乗誤差)を利用します。
※MSELoss=(1/n)Σ{(x-y)^2}=(2つの要素の差の2乗和)/(全要素数)
そして最適化アルゴリズムには毎度おなじみのSGD(確率的勾配降下法)を採用しました。

'''学習'''
for i in range(201):
  model.train()
  loss_train = 0
  for j, (x, t) in enumerate(train_loader):
    loss = criterion(model(x), t.to(device))
    loss_train += loss.item()
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
  loss_train /= j+1
  record_loss_train.append(loss_train)
  if i%10 == 0:
    print("Epoch:", i, "Loss_Train:", loss_train)
    predicted = list(input_data[0].reshape(-1))
    model.eval()
    with torch.no_grad():
      for i in range(n_sample):
        x = torch.tensor(predicted[-n_time:])
        x = x.reshape(1, n_time, 1)
        predicted.append(model(x)[0].item())
    plt.plot(range(len(sin_x)), sin_x, label="Correct")
    plt.plot(range(len(predicted)), predicted, label="Predicted")
    plt.legend()
    plt.show()

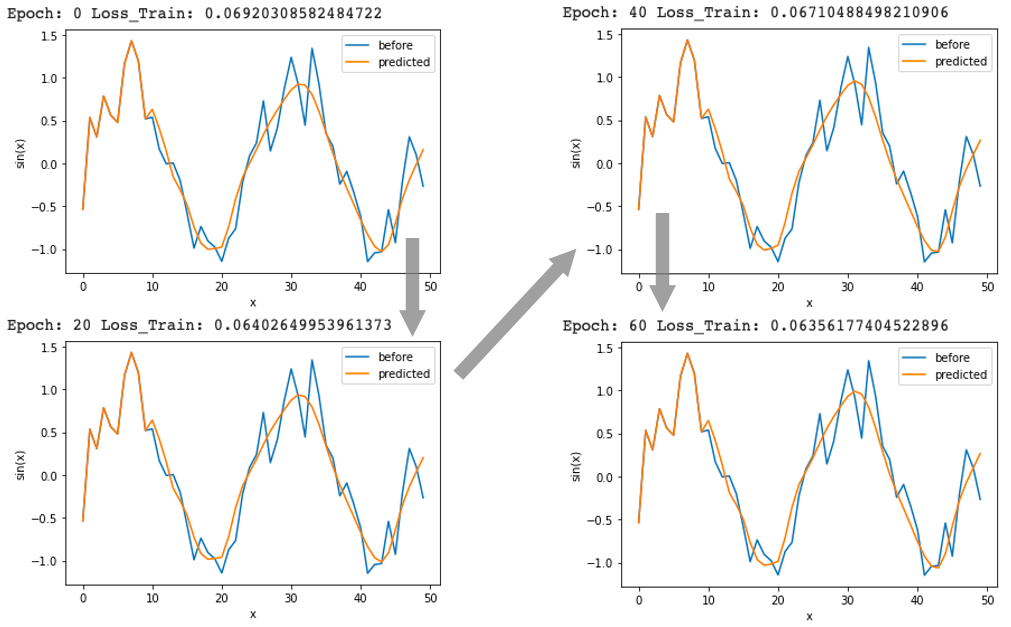
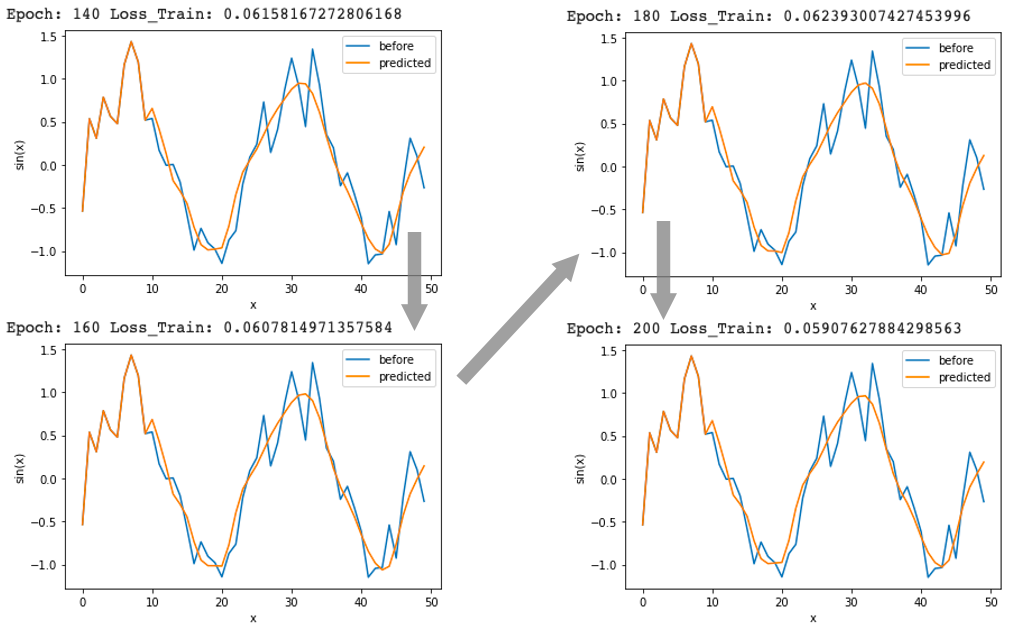
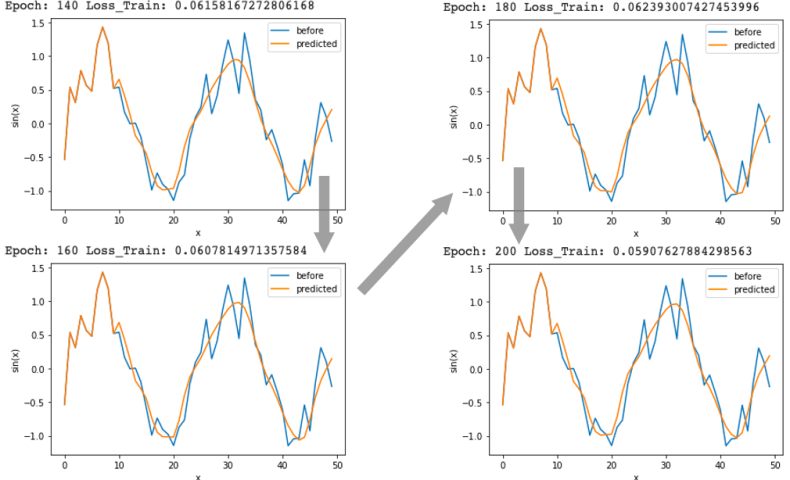
処理を回すごとに（epoch数が増えるごとに）lossの値が小さくなり、オレンジ色の予測値がどんどんsin波に近づいています。
それではモデルが機能していることが確認できたので、コードの中身をみていきましょう。
まず、ミニバッチを扱う上でmodel.train(), model.eval()で、訓練モード/評価モードの切り分けがされているかを確認します。
上から2つ目のfor文を見てみると、enumerate()が使われていますが、これは「インデックス番号 + データ」を取得するという役割です。
train_loaderには5バッチ分存在する（全体が40データで、8データ=1バッチ）ので「for j, (x, t) in enumerate(train_loader)」では、jは「0~4」の値、xは「10個の時系列データ」がまとまった1つのデータ、tは「1つの正解値」が参照されることとなります。
このfor文の中で予測値model(x)と正解値tの誤差が計算されていますが、このとき「model(x)はGPUで実行されている」ので「tも.to(device)でGPUへ移行させる」必要があります。
そしてこの後はいつも通り「勾配クリア -> 誤差逆伝播 -> パラメータ更新」の記述を加え、loss_trainで求めた誤差を用意した配列(record_loss_train)へ追加します。
次はif文の中身を見ていきましょう。
まず「1つのtensorで表された10×1の配列が、10個のtensorとしてリスト化されたもの」をpredictとして定義します。
ここで最初の時系列データが用意できたので、model.eval()で評価モードに入りデータの学習を進めます。
最後のfor文では初めに、入力xに対して「直近10個のtensorデータを1つのtensorにまとめ、モデルが読み込める(1, 10, 1)のサイズにする」という処理を施しました。
＜余談＞
「再び10個のtensorを1つのtensorにするのであれば、初めからlistなど使わずに1つのtensorとして扱えば良いのでは？」という声が聞こえてきそうですが、それではうまくいきません。
1つのtensorにするということは参照できるデータが1つになってしまうので、predicted[-10:]で動的に直近10個の値を参照することができないのです。
そもそもinput_dataは1つのデータで10個の値がまとまったものなので、それを一度解体しリスト化する（10個の独立した値として扱えるようにする）必要があります。
このリストにどんどん予測値を追加することで、直近10個の値を参照しながら学習を進められるというわけです。
ここでは「1~10番目の時系列データをそれぞれ独立した値としてリスト化 -> その10個の時系列データから11番目を予測 -> 今度は2~11番目のデータから12番目を予測 -> 次は3~12番目のデータから13番目を予測」という作業を最後(40番目)まで繰り返す流れになっています。

'''精度の確認'''
print('初めの誤差：', round(record_loss_train[0]*100,2), '%')
print('最終誤差　：', round(record_loss_train[-1]*100,2), ' %')
plt.plot(range(len(record_loss_train)), record_loss_train, label='Train')
plt.legend()
plt.xlabel('Epochs')
plt.ylabel('Error')
plt.show()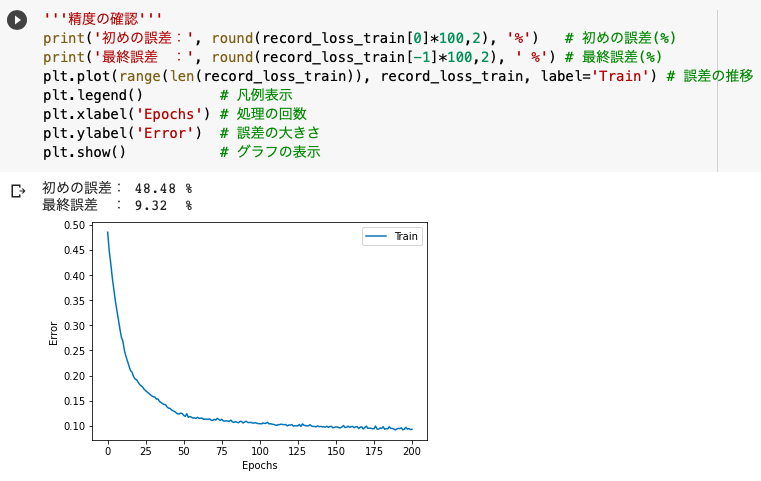

訓練を重ねていくうちに誤差を48.48%から「9.32%」まで小さくすることができました。
RNNの威力恐るべし・・

参考文献

RNN
RNNとLSTMの構造
第6回　RNN（Recurrent Neural Network）の概要を理解しよう（TensorFlow編）
【NumPy入門 np.random.normal】正規分布に従う乱数の作り方！
RNNに触れてみよう：サイン波の推測 (1/2)
RNNに触れてみよう：サイン波の推測 (2/2)
初心者のRNN(LSTM) | Kerasで試してみる
再帰型ニューラルネットワークの「基礎の基礎」を理解する　～ディープラーニング入門｜第3回