こんにちは、小郷です。
昨今は社会が複雑化したために、YesかNoか、白か黒かで片づけられない命題が増えてきたように感じます。とはいえ合格か不合格か、買うか買わないかなど、二種類の結果になる事象の予測をしたい場面は多いかなと思います。そうした予測を助けてくれるのが、ロジスティック回帰と呼ばれる種類の分析です。本記事で簡単な概要について説明していきます。
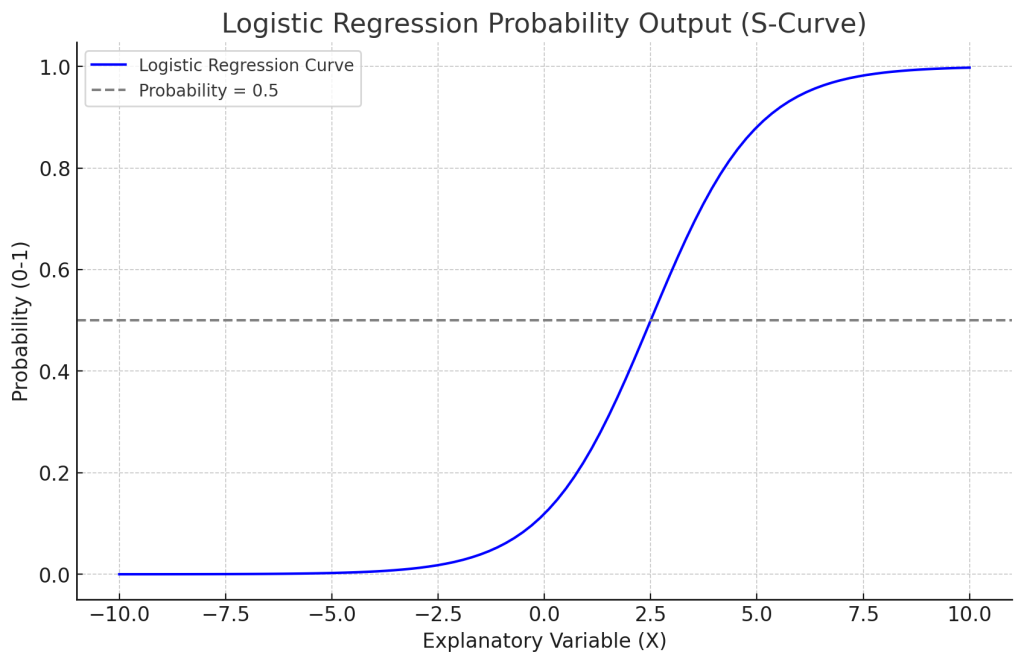
シグモイド曲線
以下のようなS字型の曲線をシグモイド曲線と呼びます。ロジスティック回帰では、この曲線を使って二値の確率を表現します。この曲線は、説明変数がある水準を超えると急激に1に近づく性質を持っており、0~1の範囲で出力される確率として解釈できます。
ロジットの概念
確率をオッズに変換したもので、さらにオッズの対数をとったものです。順番に説明していきます。
オッズとは
「ある事象が起こる確率」と「起こらない確率」の比率を表す値です。以下の式で表されます。
$$ \frac{p}{1 – p} $$
\(p\): ある事象が起こる確率。0~1の値で表される。
ロジットは、オッズの自然対数をとったものです。これにより、0〜1の範囲に限らず、-∞〜∞の値を取ることができ、線形回帰のアプローチを行うことができるようになります。説明変数が変わったときに発生確率(0~1の範囲)がどのように変化するかを示す指標です。
$$ \log(\frac{p}{1 – p})$$
ロジットは以下の式に従うことが前提です。以下の数式と似たようなものは前回の重回帰分析の記事でも登場しました。求め方には違いがあり、重回帰分析では各係数は最小二乗法で求めますが、ロジスティック回帰では尤度最大化法(MLE)で求めます。
$$ \log(\frac{p}{1 – p}) = \beta _0 + \beta _{1}x_{1i} + \beta _{2}x_{2i} + … + \beta_{p}x_{pi} $$
ただし、明確に以下の点で異なります。
– 目的変数: 重回帰は目的変数が連続値ですが、ロジスティック回帰は目的変数が(基本は)二値です。
– 出力: 重回帰は連続値を出力し、ロジスティック回帰は確率を出力します。
モデルも異なります。係数の求め方も変わってくるので、次の項目で解説します。
重回帰
$$ Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \ldots + \beta_p X_p + \varepsilon $$
ロジスティック回帰
$$ P(Y=1|X) = \frac{1}{1 + e^{-(\beta_0 + \beta_1 X_1 + \beta_2 X_2 + \cdots + \beta_p X_p)}} $$
MLEによる係数の求め方
今回も2変数のモデルを考えて、簡単に求めてみましょう。
$$ P(Y=1|X) = \frac{1}{1 + e^{-(\beta_0 + \beta_1 X_1 + \beta_2 X_2)}} $$
\(Y\): 0または1を取る目的変数
\(X_1, X_2\): 説明変数
\(\beta_1, \beta_2\): 係数
\(\beta_0\): バイアス項
確率関数の定義
これをまず、Yが1および0をとる確率の式に変形します。
シグモイド関数は以下の定義で与えられるため、先のモデルを当てはめると以下のように書けます。
$$ \sigma(z) = \frac{1}{1 + e^{-z}} $$
$$ P(Y=1|X) = \sigma(\beta_0 + \beta_1 X_1 + \beta_2 X_2) $$
Yが0になる確率とYが1になる確率の合計は1になり、以下のような式で表すことができます。
$$ P(Y=0|X) = 1 – P(Y=1|X) $$
つまり、Yが0になる確率と、1になる確率は以下の二種類の式で表すことができます。
$$ P(Y=0|X) = 1 – \sigma(\beta_0 + \beta_1 X_1 + \beta_2 X_2) $$
$$ P(Y=1|X) = \sigma(\beta_0 + \beta_1 X_1 + \beta_2 X_2) $$
シグモイド関数の性質として、以下の式が成り立ちます。
$$ 1 – \sigma(z) = \frac{e^{-z}}{1 + e^{-z}} $$
よって、\(P(Y=0|X)\)は以下のようにも書けます。
$$ P(Y=0|X) = \frac{e^{-(\beta_0 + \beta_1 X_1 + \beta_2 X_2)}}{1 + e^{-(\beta_0 + \beta_1 X_1 + \beta_2 X_2)}} $$
尤度関数の定義
尤度とは、データが実際に観測されたとき、「それがどのくらいあり得るか?」を表す値です。
例えば、コインの表が出る確率が50%と仮定して、10回投げて10回面が出たとします。その場合は以下の式で定義できます。確率pの冪乗で求めることができます。
$$ L(p) = p^{10} (p = 0.5)$$
裏になった試行を加味、つまり試行の母数を加味する場合は以下の式で表せます。n回コインを投げて、k回表が出る試行を一回行った場合の尤度という意味を持ちます。
$$ L(p) = \binom{n}{k} p^k (1 – p)^{n – k} $$
\(\binom{n}{k}\)は、「\(n\)回中\(k\)回成功する組み合わせの数」であり、\(\frac{n!}{k!(n-k)!}\)で求められます。
複数回の試行を行った場合のトータルの尤度は以下です。
$$ L(p) = \prod_{i=1}^{m} \binom{n_i}{k_i} p^{k_i} (1 – p)^{n_i – k_i} $$
先に求めたY=1になる確率は以下で表せます。
$$ P(Y_i|X_i) = P(Y_i = 1|X_i)^{Y_i}・P(Y_i = 0|X_i)^{1 – Y_i} $$
観測された\(Y_i\)が1であるならば、\(1 – Y_i\)は0になるため、最終的な式は以下になります。
$$ P(Y_i|X_i) = P(Y_i = 1|X_i)^{Y_i} $$
観測された\(Y_i\)が0であるならば、\(P(Y_i = 1|X_i)^{Y_i}\)は1になるため、最終的な式は以下になります。
$$ P(Y_i|X_i) = P(Y_i = 0|X_i) $$
これに、先ほど求めた確率の式を代入すると以下になります。
$$ P(Y_i|X_i) = \sigma(\beta_0 + \beta_1 X_1 + \beta_2 X_2)^{y_i}・(1 – \sigma(\beta_0 + \beta_1 X_1 + \beta_2 X_2))^{1 – y_i} $$
上記の関数に対して、尤度関数を作ってみましょう。 先に完成した式を示します。
$$ L(\beta_0, \beta_1, \beta_2) = \prod_{i=1}^{n} \left( \sigma(\beta_0 + \beta_1 X_{i1} + \beta_2 X_{i2})^{y_i} \cdot (1 – \sigma(\beta_0 + \beta_1 X_{i1} + \beta_2 X_{i2}))^{1 – y_i} \right)$$
\(\sum\)は全ての値の和を表すのに対して、\(\prod\)は全ての値の積を示します。
iはサンプル番号を表します。複数のサンプルを集めてきて、この式に代入を行うことで\(\beta_0, \beta_1, \beta_2\)を求められるようになります。計算しやすくするために、以下の対数尤度関数をとることが一般的です。
$$ \ell(\beta_0, \beta_1, \beta_2) = \sum_{i=1}^{n} \left( y_i \log(\sigma(\beta_0 + \beta_1 X_{i1} + \beta_2 X_{i2})) + (1 – y_i) \log(1 – \sigma(\beta_0 + \beta_1 X_{i1} + \beta_2 X_{i2})) \right) $$
最急降下法でパラメータ推定
以下の式で、勾配を計算します。微分が接線の勾配を求めるという性質は、回帰シリーズの第一回の記事で紹介しているため、そちらをご確認ください。
$$ \frac{\partial \ell}{\partial \beta_j} = \sum_{i=1}^n (y_i – \sigma(\beta_0 + \beta_1 X_{i1} + \beta_2 X_{i2})) X_{ij} $$
\(j = 0,1,2\)は各パラメータを指します。
以下の反復式でパラメータを更新し、収束するまで続けます。
$$ \beta^{(t+1)} = \beta^{(t)} + \alpha \nabla \ell(\beta^{(t)}) $$
\(\alpha\)は学習率と呼ばれ、更新ステップの大きさを決定します。初期設定は0.001、0.01などがよく使われ、試行錯誤してみると良いです。訓練が進むにつれて値を小さくしていくようなやり方もあります。
対数尤度関数が一定の閾値以上の変化をしなくなったら、収束したと言って良いでしょう。
タイタニック号の悲劇
ここからはデータを使って、説明変数の変化に応じて係数(回帰係数)がどのように推定されるかを見ていきましょう。
1912年4月10日に処女航海としてタイタニック号はイギリス・サウサンプトンからアメリカ・ニューヨークに向けて出航しました。北大西洋で氷山に激突したのは、4月14日のことでした。船体は船首から沈んでいったと言われています。
この悲劇では、1,513人の犠牲者が出ました。この事故には、性別や年齢、乗客の等級(チケットクラス)といったさまざまな要因が生存率に影響したと言われています。左舷側では一等客室の「女性と子供を優先する」という対応が取られたということが判明していますが、その結果は実際に数値として現れるのでしょうか。
このようなデータを用いることで、「ある乗客が生存したかどうか」をロジスティック回帰を使って予測できるか試してみましょう。
今回の分析にはOpenMLのデータセットを用いました。
https://api.openml.org/d/40945
変数の定義
今回の目的変数は「生死」の値で、説明変数は以下を選択しました。サクッとPythonコードで処理してみましょう。今回は欠損値を、仮の値でカバーしています。
– 年齢
– 運賃
– 客室等数
– 同乗の兄弟・配偶者数
– 同乗の親・子供数
– 性別が男性かどうか
– 出港地がQueenstown
– 出港地がSouthampton
# データ読み込みと前処理
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, classification_report
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
# データ読み込みと前処理
titanic_data = pd.read_csv('ファイルパス', na_values="?")
titanic_data_cleaned = titanic_data.drop(columns=["name", "ticket", "cabin", "boat", "body", "home.dest"])
# 欠損値処理
titanic_data_cleaned['age'].fillna(titanic_data_cleaned['age'].median(), inplace=True)
titanic_data_cleaned['fare'].fillna(titanic_data_cleaned['fare'].mean(), inplace=True)
titanic_data_cleaned.dropna(inplace=True)
# カテゴリ変数のダミー化(性別、出港地など)
titanic_data_cleaned = pd.get_dummies(titanic_data_cleaned, columns=['sex', 'embarked'], drop_first=True)
# 特徴量とターゲット変数の分割(複数変数使用)
X = titanic_data_cleaned[['pclass', 'age', 'fare', 'sibsp', 'parch', 'sex_male', 'embarked_Q', 'embarked_S']]
y = titanic_data_cleaned['survived']
# トレーニングとテストの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 標準化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# ロジスティック回帰モデルの訓練
logreg = LogisticRegression(max_iter=1000)
logreg.fit(X_train, y_train)
# モデルの予測と評価
y_pred = logreg.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
classification_rep = classification_report(y_test, y_pred)
# 結果の表示
print("Accuracy:", accuracy)
print("Classification Report:\n", classification_rep)
# 各変数の寄与度(係数)を表示
coefficients = pd.DataFrame({
'Feature': X.columns,
'Coefficient': logreg.coef_[0]
})
# 寄与度を確認
print(coefficients)
# 寄与度を棒グラフで表示
plt.figure(figsize=(10, 6))
plt.barh(coefficients['Feature'], coefficients['Coefficient'], color='skyblue')
plt.xlabel("Coefficient")
plt.title("Feature Coefficients in Logistic Regression Model")
plt.grid(True)
plt.show()
各変数がどのような利き方をしているかを図示しています。
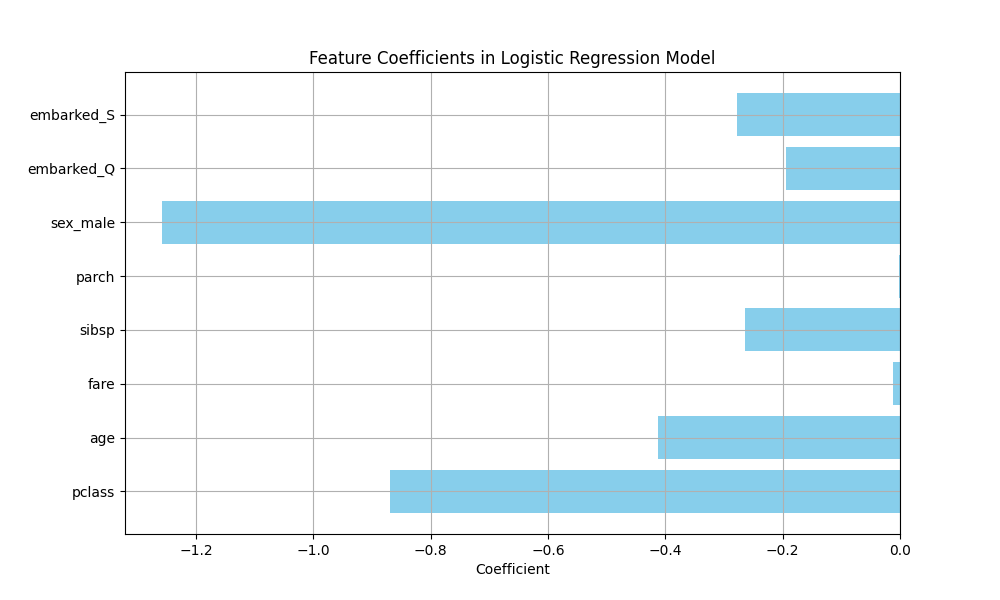
Feature Coefficient
0 pclass -0.868982
1 age -0.412035
2 fare -0.011350
3 sibsp -0.264983
4 parch -0.000923
5 sex_male -1.257962
6 embarked_Q -0.194921
7 embarked_S -0.277552
ここから明確にわかることは以下です。右舷か左舷かの情報はありませんが、「女性と子供を優先する」という対応が効いていることが示唆されました。
– sex_male: 男性であることは、生存率を著しく下げる
– pclass: 客室等数(1〜3)が上がるほど生存率を下げる
– age: 年齢が上がるほど生存率を下げる
モデルの関数を見てみましょう。
import numpy as np
# モデルの切片と係数を取得
intercept = logreg.intercept_[0]
coefficients = logreg.coef_[0]
# 特徴量名を取得
feature_names = X.columns
# 数式の組み立て
terms = [f"({coef:.3f} * {name})" for coef, name in zip(coefficients, feature_names)]
equation = " + ".join(terms)
model_function = f"P(y=1|X) = 1 / (1 + exp(-({intercept:.3f} + {equation})))"
# 出力
print("ロジスティック回帰モデルの関数:")
print(model_function)
ロジスティック回帰モデルの関数:
P(y=1|X) = 1 / (1 + exp(-(-0.685 + (-0.869 * pclass) + (-0.412 * age) + (-0.011 * fare) + (-0.265 * sibsp) + (-0.001 * parch) + (-1.258 * sex_male) + (-0.195 * embarked_Q) + (-0.278 * embarked_S))))ページからはみ出しそうな予感しかないですが、Latexで書くと以下です。
$$ P(y=1|X) = \frac{1}{1 + \exp\left(-\left(-0.685 + (-0.869 \cdot \text{pclass}) + (-0.412 \cdot \text{age}) + (-0.011 \cdot \text{fare}) + (-0.265 \cdot \text{sibsp}) + (-0.001 \cdot \text{parch}) + (-1.258 \cdot \text{sex_male}) + (-0.195 \cdot \text{embarked_Q}) + (-0.278 \cdot \text{embarked_S})\right)\right)} $$
では、サンプルデータを入れてみましょう。
# 1人分のテストデータ
# 新しい人物データ(pclass, age, fare, sibsp, parch, sex_male, embarked_Q, embarked_S の順に入力)
# 例: 1等級, 31歳, 7.25の運賃, 兄弟姉妹なし, 親なし, 男性, クイーンズタウンから出港
new_person = np.array([[1, 31, 7.25, 0, 0, 1, 0, 1]])
# データを標準化
new_person_scaled = scaler.transform(new_person)
# 生存確率と死亡確率を取得
probabilities = logreg.predict_proba(new_person_scaled)
# 結果表示
print("死亡確率:", probabilities[0][0])
print("生存確率:", probabilities[0][1])
結果は以下のようになりました。生き残れる確率の方が低そうですね。
死亡確率: 0.5764573020875579
生存確率: 0.42354269791244215終わりに
二値と言えば「やるか」「やらないか」のような決断は、現代人を日々悩ませていると思います。実は我々は、一日に35,000回もの決断をしていると言われていて、決断のたびに疲労は溜まっていくことがわかっています。夜になるほど、衝動的な決断をする傾向もあるようです。
こうした決断コストを少しでも低減させる方法として、我々人間は「ヒューリスティック」というものを使っています。例えば利用可能性ヒューリスティックは、耳にしたことがあること、見たことがあることを選んでしまう傾向のことを言います。この前も衆議院選挙がありましたが、選挙カーが政策を言わずに名前だけ連呼しているような現象を目の当たりにしたかもしれません。テレビCMで見たことのある商品を買ってしまうこともあると思います。これは全て利用可能性ヒューリスティックと呼ばれるものです。そしてヒューリスティックな判断は、それが必ずしも最適解ではないとされています。
頭の中で買うか買わないかという決断をする際に、今回紹介したような推定を頭の中に埋め込んだコンピュータが一瞬で行ってくれる、SFな世界が早くきて欲しいと個人的には思っています。マーケティングの常識はガラリと変わってしまいそうですが。













