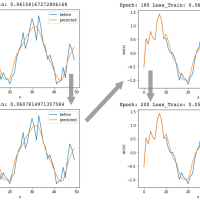
こんにちは、小郷です。回帰と言えばフリードリヒ・ニーチェの永劫回帰を思いつくので、上記のタイトルとサムネにしました。
回帰分析という言葉を聞いたことはあるでしょうか。聞いたことはなくても、エクセルを使ってx軸とy軸に何らかの値を置いて散布図を作り、そこに直線を引いた経験がある方は多いと思います。あの直線のことを回帰直線と呼びますが、それを引くためにどのような計算が行われているのかは、その使用頻度の割にはよく知られていないと思います。
そこで本記事では、今更ではありますが回帰分析をおさらいするとともに、利用シーンや注意点について解説していきたいと思います。
概念と歴史
回帰の概念は19世紀、黎明期の遺伝学者であるフランシス・ゴルトンによって作られました。『種の起源』で有名なチャールズ・ダーウィンの従兄に当たる人物です。ゴルトンが提唱した優生学は今でこそ歴史の汚点となっていますが、実は統計学の発展は優生学の証明に影響を受けており、ピアソンやフィッシャー等の統計学・遺伝学の著名人も彼の影響を受けていると言われています。なお、同じく統計学の偉人として知られるフローレンス・ナイチンゲールとゴルトンは遠縁にあたります。
回帰分析とは、簡単に言えば「得られたデータの背景に存在する規則性を、変数を用いて説明する」分析です。感覚的にわかりやすい例としては、体重は身長が高いほど重くなる傾向にありますが、この場合に身長は体重に対する説明変数と見做すことができます。また、説明される側の変数、つまり体重を応答変数と呼びます。
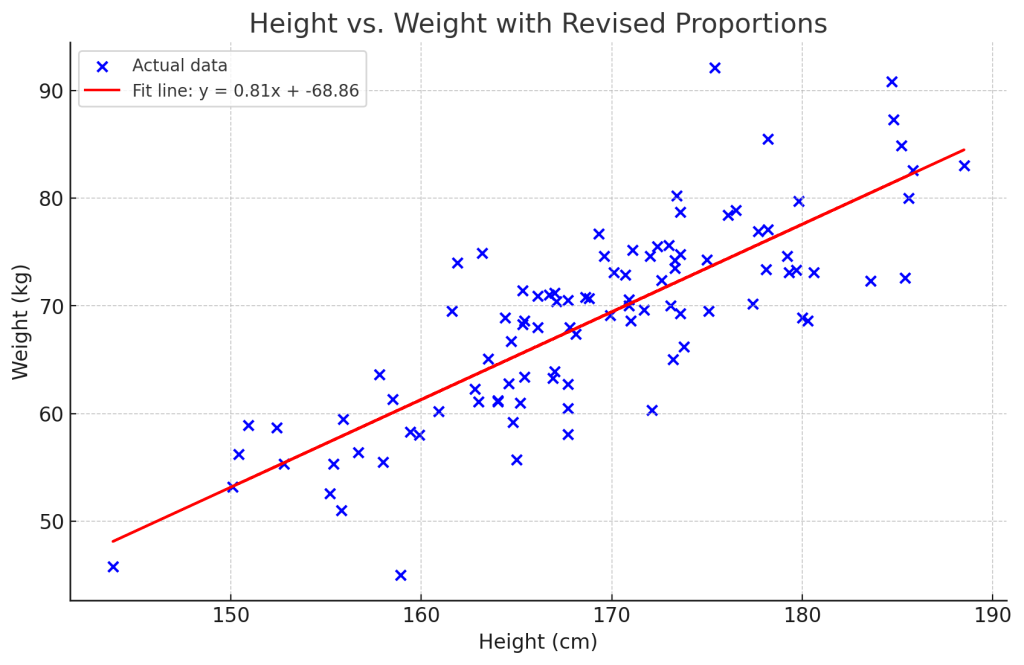
Python使ってそれっぽいデータを作ってみました。体重をy軸、身長をx軸に配置しています。青いバッテンが個体のデータ、赤い線が回帰直線です。この回帰直線を書くために、 y = 0.81x – 68.86という一次関数が与えられていますが、これを線形単回帰モデルと呼びます。この式における、0.81と-68.86という係数を求めることが回帰分析の肝です。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 乱数のシードを再設定
np.random.seed(42)
# データの個数
num_samples = 100
# 身長データを生成(平均170cm、標準偏差10cm)
heights = np.random.normal(170, 10, num_samples)
# 体重データを生成する新しいパラメータ(現実的な範囲に調整)
slope = 0.7 # 身長あたりの体重増加量を減らす
intercept = -50 # 切片を調整して全体の体重を下げる
weights = slope * heights + intercept + np.random.normal(0, 5, num_samples)
# DataFrameを作成
data = pd.DataFrame({
'Height (cm)': np.round(heights, 1),
'Weight (kg)': np.round(weights, 1)
})
# Linear regression model
model = LinearRegression()
X = data['Height (cm)'].values.reshape(-1, 1) # Reshaping for sklearn
y = data['Weight (kg)'].values
# Fit the model
model.fit(X, y)
slope = model.coef_[0]
intercept = model.intercept_
# Generate predictions
data['Predicted Weight (kg)'] = model.predict(X)
# Plotting
plt.figure(figsize=(10, 6))
plt.scatter(data['Height (cm)'], data['Weight (kg)'], color='blue', label='Actual data')
plt.plot(data['Height (cm)'], data['Predicted Weight (kg)'], color='red', label=f'Fit line: y = {slope:.2f}x + {intercept:.2f}')
plt.xlabel('Height (cm)')
plt.ylabel('Weight (kg)')
plt.title('Height vs. Weight with More Realistic Proportions')
plt.legend()
plt.grid(True)
plt.show()
先に出てきた変数の名称は、以下のような言い換えが使われることもあります。
- 説明変数: 独立変数・予測変数・共変量
- 応答変数: 目的変数・被説明変数・従属変数・基準変数
一次関数の最も簡単な例
中学数学の領域に置いて、あらかじめ直線に乗るデータが複数与えられていて、そのデータを説明する直線を求めるような問題は一般的かと思います。
例えば以下のような(現実的にはあり得ないものの)、テストの得点が勉強時間に比例するような結果が得られたとします。
| 勉強時間 (時間) | テストの得点 |
|---|---|
| 1 | 50 |
| 3 | 70 |
| 5 | 90 |
この手の問題の解き方として、y = ax + bと式を置いて、異なる2ポイントの結果をxとyに代入し、aとbを求めるやり方が最も簡単でしょう。
まずはa(勾配)を求めましょう。
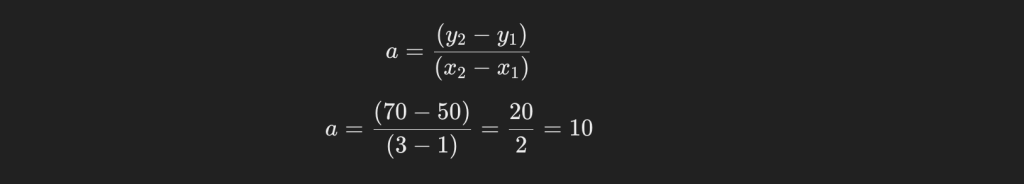
続いてb(切片)を求めます。
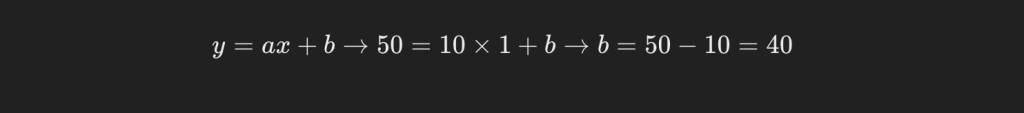
これにより、得られているデータを説明する一次関数が以下のように求められました。
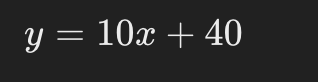
また、勾配と切片を回帰係数と呼びます。
単回帰分析
しかし、現実に得られているデータは先の単純な一次関数の上に乗るはずもなく、ある程度のばらつきが出ます。では、先に示した身長と体重の関係性のように、ばらつきがある散布図に対して回帰直線を引くことは、どのような手段で実現できるのでしょうか。
最もポピュラーな手法として、最小二乗法が知られています。全てのデータ点と回帰直線との距離が最小になる傾きと切片を数学的に求める手法です。
カジュアルに表現すると、各点から一番近い線を引いたらそれっぽい線になるよね、という事です。
ちょっとややこしい内容ですが、単回帰だけでなく、別記事で解説予定の重回帰分析においても重要な概念です。詳しく、しかし極力わかりやすく説明していきます。
最小二乗法
推定される回帰直線で得られたy軸の値と、観測されたデータで得られたy軸の値との差を残差と呼び、以下のように表されることが一般的です。
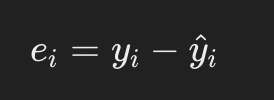
ここで、yハットは回帰直線を用いて推定されたi番目の値を指します。統計学では予測値や推定値に対してハットを付与して表すのが一般的です。図の破線の部分が残差です。
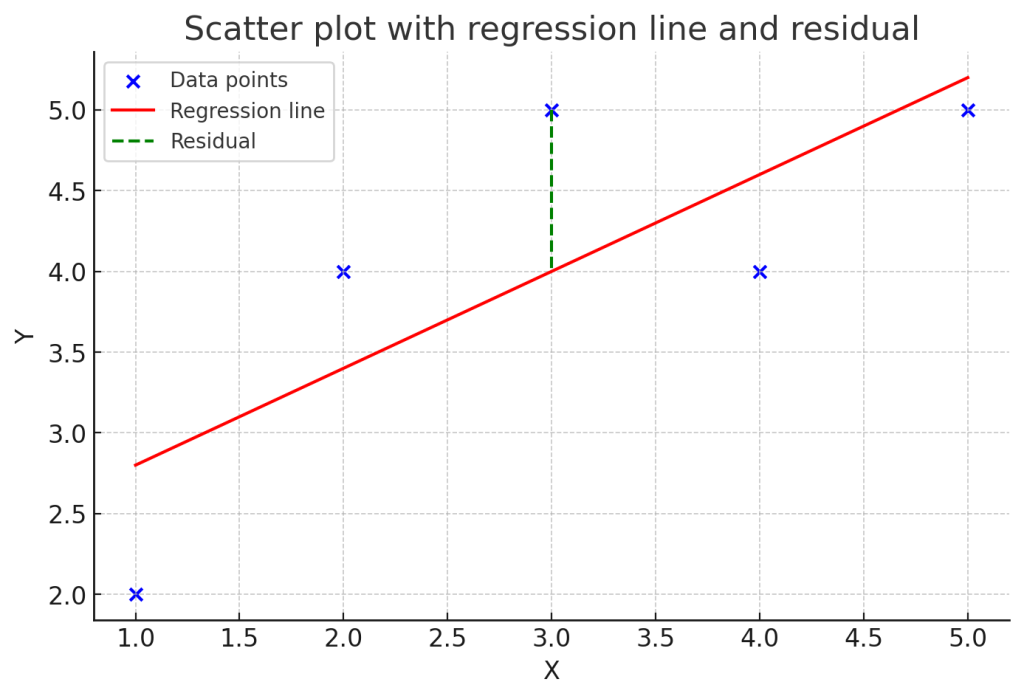
この残差の二乗和(残差平方和)を最小化するような回帰係数を導出する方法が、最小二乗法です。以下に残差平方和の一般式を示します。
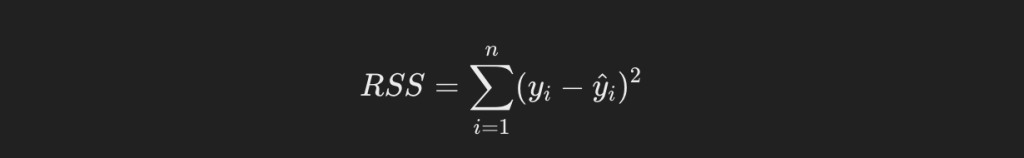
しかし、現時点で回帰直線がわかっていないので、yハットもわかりません。しかし計算上、yハットは傾きと切片と説明変数の式で表すことができます。それを代入すると、残差平方和は以下のようになります。
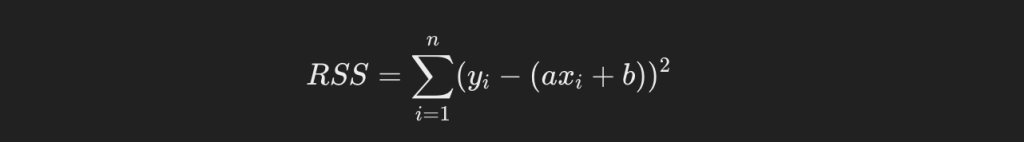
偏微分
この式のa及びbに対して、偏微分を行います。偏微分とは、複数の変数が含まれる関数に対し、1つの変数だけに着目して他の変数は全て定数として扱い、微分することです。
関数f(x) = x^2を偏微分してみましょう。変数が1つの式に対する微分は一般に全微分と呼ばれますが、概念を理解しやすくするために偏微分の文脈で解説を進めます。
偏微分をする際の式は一般に、以下のように記述されます。
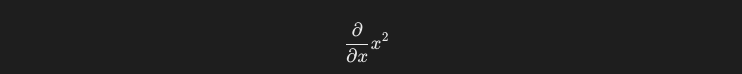
これを、微分の基本的なルールに従うと、以下のように計算することができます。
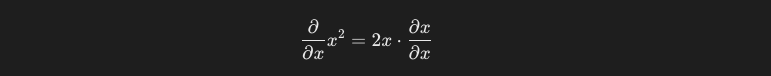
xをxで微分した際の結果は1になります。よって、x^2をxで微分した結果は、2xとなります。
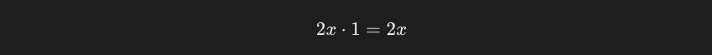
この計算を、残差平方和の式に対しても行います。まずはaに関して偏微分をした計算結果は以下のようになります。
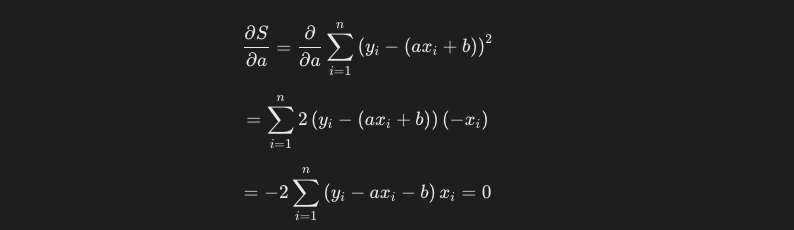
bに関して偏微分を行います。
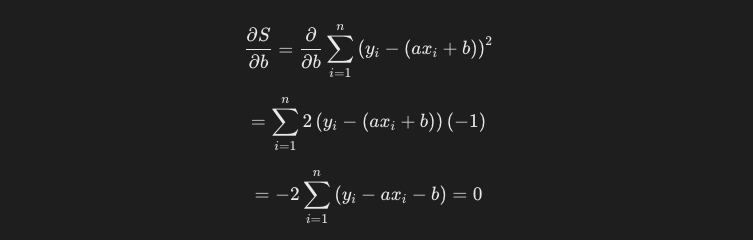
ここで、偏微分をした結果が0と等しいと定義しているのは、極値を求める際の一般的な方法です。
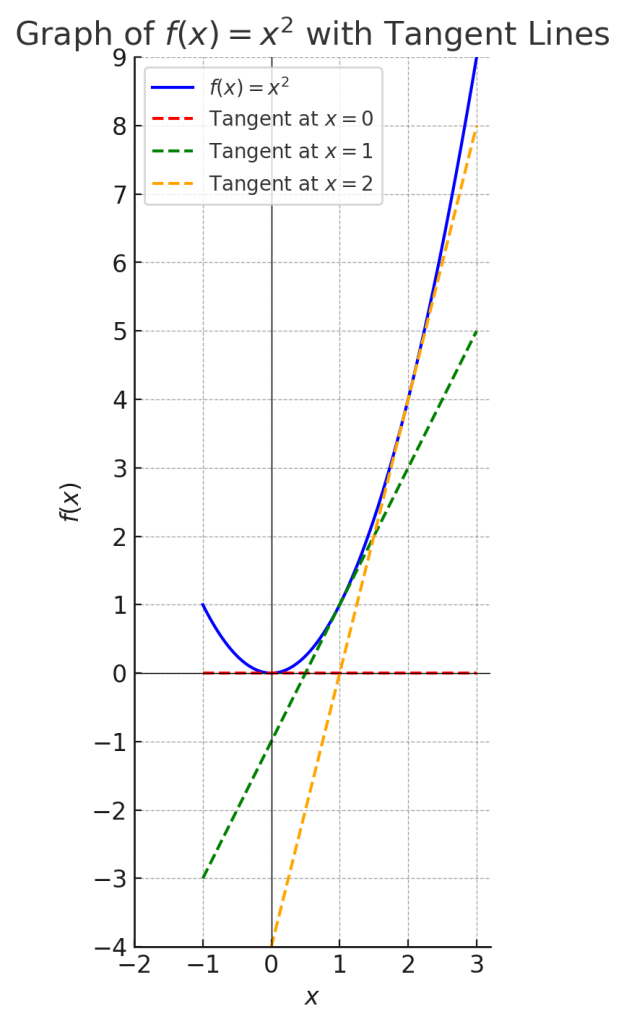
以下にx^2のグラフを示します。破線はそれぞれ接線です。一般に接線の傾きは、微分により得ることができます。x^2を微分した結果である2xは、xのそれぞれの点における接線の傾きを示しています。極値、 すなわちx^2 = 0となる時、傾きは0となっています。
これを最小二乗法の計算に適用すると、残差平方和をaまたはbで偏微分をした値(=接線の傾き)が0であれば、残差平方和を最小にするaまたはbの値を求めることができる、というわけです。
方程式を整理し、連立方程式とします。
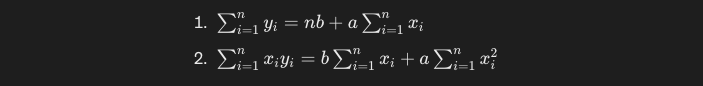
y_iとx_iのそれぞれの値を、偏差 + 平均の式に変換します。
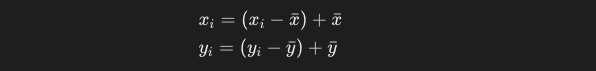
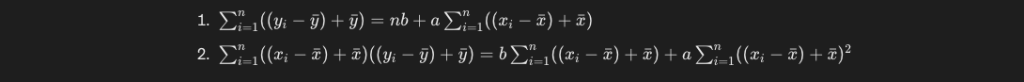
この式を整理すると、以下のようになります。
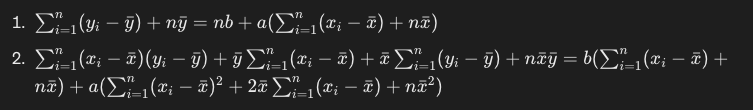
ここで以下のポイントを押さえると、より式が簡単になります。
- シグマ式の内部の定数は、n×定数として外に出せる。yバーと、nxバーは外に出すことができます。
- 偏差の合計は、0になります。
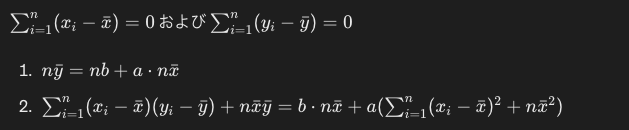
最終的に両辺を約分すると、以下の式が求められます。yとxの各データポイントさえ分かっていれば、簡単な計算で回帰係数a及びbを求めることができ回帰直線も定めることができるようになりました。
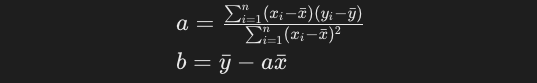
なお、aの分母をn(またはn-1)で割るとxの分散に、aの分子をn(またはn-1)で割るとxとyの共分散になります。
決定係数
いわゆるR2乗値と呼ばれるもので、回帰分析においてモデルの適合度を示す統計的指標です。y hatは回帰直線に変換することもできます。
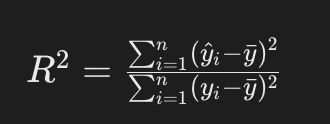
以下の性質を持ちます。
- 1に近いほど、説明変数が応答変数の変動をよく説明している。
- 1に近ければ必ずしも良いモデルというわけではなく、機械学習の文脈では過学習をしている可能性も考え、別の指標でモデルを評価する必要がある。
簡単な計算をしてみる
学生の勉強時間とテストの点数が以下のように与えられたとします。勉強時間を説明変数、テストの得点を応答変数とした回帰直線を求めてみましょう。基本の式は前項までで得られているので、当てはめるだけです。
| 学生 | 勉強時間 (x) | テストの得点 (y) |
|---|---|---|
| 1 | 2 | 50 |
| 2 | 3 | 55 |
| 3 | 5 | 65 |
| 4 | 7 | 70 |
| 5 | 8 | 80 |
xとyの平均は以下の通りです。

各データ点について残差を求めていきましょう。
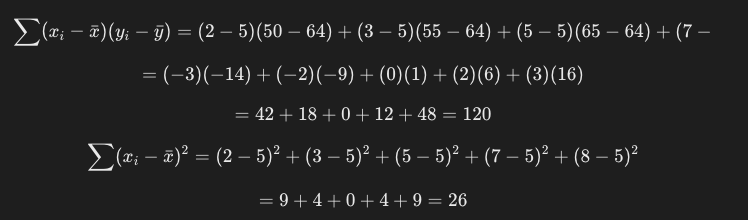
これを先ほどの式に当てめると、以下の値が求められます。
a = 4.615
b = 40.925
よって、y = 4.615x + 40.925という回帰直線が得られました。図にしてみると以下です。
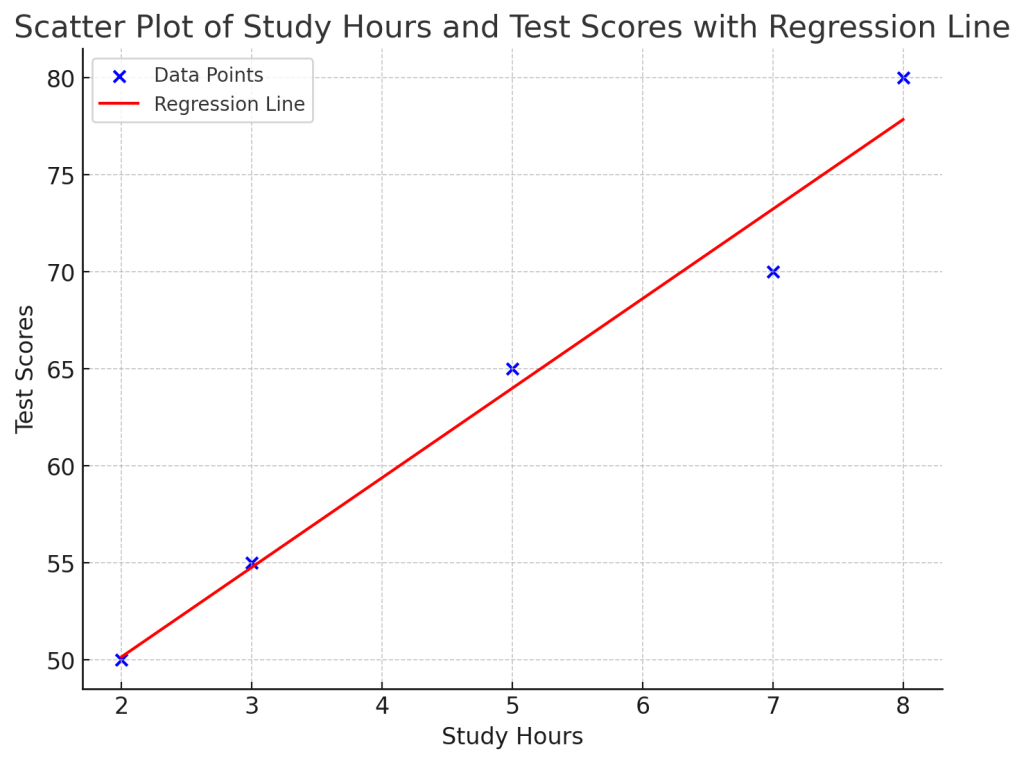
使い所
基本的に説明変数が目的変数をどの程度説明しているかを示してなんらかの示唆を得たい際には、大体使うことができます。以下に例を示します。扱う要素が少ないことで、シンプルに考えることができる事は明確な利点です。
- 収入と家計消費の関係
- 温室効果ガス排出量と平均気温の関係
- 広告費用と売上の関係
- 顧客満足度スコアとリピート購入率の関係
しかし、現実に存在するデータは複数の説明変数が複雑に絡み合っていることが殆どです。例えば体重を説明する要素には、先に挙げた身長以外にも以下の要素があります。
- 骨格筋率
- 体脂肪率
- 肥満度
一般的な感覚として、骨格筋率が上がれば体脂肪率は下がり、体脂肪率が上がれば肥満度は上がるでしょう。説明変数同士が相互に関係することを多重共線性といい、これは回帰モデルを歪める要素として知られています。この辺りの話は次回の記事で解説したいと思います。
実データを使って統計量を得る、および単回帰分析を実施するには
主要なSQLデータベースには、統計用の関数が用意されています。こちらやこちらの記事で紹介した統計量についても、関数を使って簡単に計算することができます。以下に幾つかの例を示します。
BigQuery
CORR(column1, column2): 相関係数を得ることができます。
VAR_SAMP(column): 標本分散を得ることができます。
VAR_POP(column): 母分散を得ることができます。
STDDEV_SAMP(column): 標本標準偏差を得ることができます。
STDDEV_POP(column): 母標準偏差を得ることができます。
単回帰分析を実施する際には、幾つかのステップが必要です。ここでは多くを説明はしませんが、いずれ専用記事にしたいですね。通常は複数カラムをSELECT部に記述して、重回帰をやってしまうことが多いです。
-- モデルの作成
CREATE OR REPLACE MODEL `your_project.your_dataset.your_model`
OPTIONS(model_type='linear_reg') AS
SELECT
x,
y AS label
FROM
`your_project.your_dataset.your_table`;
-- 回帰係数の取得
SELECT
*
FROM
ML.WEIGHTS(MODEL `your_project.your_dataset.your_model`);
-- 予測
SELECT
*
FROM
ML.PREDICT(MODEL `your_project.your_dataset.your_model`,
(SELECT x FROM `your_project.your_dataset.your_train_table`));
Snowflake
分散や標準偏差を得る関数は共通なので割愛します。
REGR_SLOPE(y, x): 線形回帰直線の傾きを得られます。
REGR_INTERCEPT(y, x): 線形回帰直線の切片を得られます。
REGR_R2(y, x): 決定係数を得られます。
これらの指標があれば、クエリを用いて単回帰分析はできそうですね。
終わりに
普段エクセル等のツールがよしなにやってくれる線形近似ですが、ここまでに説明してきた通り、結構奥深いんですね。この辺りの話が分かっていると、機械学習モデルの構築や、より高度な多変量解析に挑戦していけるのではないかと思います。
ちなみにこれを書いている奴の願いは、小学生の頃の夏休みを永劫回帰することです。
ここまで読んでいただき、ありがとうございました。最後にちょっとだけ、メインに含めるかどうか迷った部分をオマケとして書いています。(本サイトはNoteとかじゃないので)全て無料で読むことができます。
応用編 回帰係数の区間推定
さて、今回の最小二乗法で得られた回帰係数は、データに対する真の指標なのでしょうか。ありがたいことに、こちらの記事を読んでいただいている方は、そうは思わないでしょう。現実的に得られたデータというのは、母集団から抽出された標本に過ぎません。つまり、回帰係数は選ばれた標本に左右されて値が変わる、確率変数と見なすことができます。
回帰係数には不確定性があります。例えば少ないデータで傾向を見てみたら正の相関があったが、同じ集団から別のデータを取ったら負の相関が見られた、というような事があると困るわけですね。これを避けるために、回帰係数がどのくらいの範囲にあるかを知っておくことは重要です。
以下に単回帰モデルの一般式を示します。
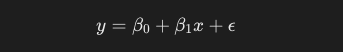
ϵは誤差項と呼ばれ、モデルが説明できないランダムな変動やノイズを表します。以下の特性を持っていると仮定します。
- 誤差項は互いに独立している。
- 平均(期待値)は0である。
- 分散は一定である
- 正規分布に従う
既出のデータセットを用いて誤差を計測してみましょう。
| 学生 | 勉強時間 (x) | テストの得点 (y) |
|---|---|---|
| 1 | 2 | 50 |
| 2 | 3 | 55 |
| 3 | 5 | 65 |
| 4 | 7 | 70 |
| 5 | 8 | 80 |
先の計算の通り、回帰直線の方程式は以下です。

残差平方和の計算
各データ点の予測値と、残差を計算します。
| x | 𝑦 | 予測値 | 残差 |
|---|---|---|---|
| 2 | 50 | 40.925+4.615×2=50.15540.925+4.615×2=50.155 | 50−50.155=−0.15550−50.155=−0.155 |
| 3 | 55 | 40.925+4.615×3=54.7740.925+4.615×3=54.77 | 55−54.77=0.2355−54.77=0.23 |
| 5 | 65 | 40.925+4.615×5=63.99540.925+4.615×5=63.995 | 65−63.995=1.00565−63.995=1.005 |
| 7 | 70 | 40.925+4.615×7=73.22540.925+4.615×7=73.225 | 70−73.225=−3.22570−73.225=−3.225 |
| 8 | 80 | 40.925+4.615×8=77.8440.925+4.615×8=77.84 | 80−77.84=2.1680−77.84=2.16 |
残差平方和は以下のように求めることができます。
RSS=(−0.155)^2+(0.23)^2+(1.005)^2+(−3.225)^2+(2.16)2=16.154
標準誤差の計算
傾きの標準誤差は、以下の式で求めることができます。どうしてこのような式になるのかを、追って解説します。

ここで、回帰直線の切片と傾きという2つのパラメータが決まるので、残差の自由度はデータ数から2を引いたものになります。残差平方和を自由度で割ると、誤差項の分散の不偏推定量が得られます。
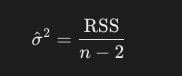
次に、傾きの分散は以下の式で求めることができます。xの偏差平方和を分母にしているのは、回帰係数の推定値の標準誤差を適切に評価するためです。xの散らばりが大きい、つまりデータポイントが広く分布しているデータであるほど、モデルがデータの傾向をより正確に捉えることができます。
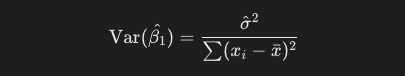
これの平方根を取ったのが、先の標準誤差です。今回のデータでは、約0.455になります。
信頼区間の計算
今回は95%信頼区間を計算します。サンプルサイズが小さい場合に、標本平均の分布は正規分布には従わず、t分布に従うとされます。標本の標準偏差を用いた分布が、真の分布を過小評価することが知られています。
今回は自由度3のt分布表に従い、t値を3.182と置いて、以下の一般式に当てはめます。
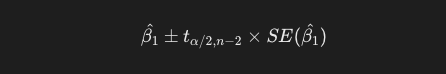

したがって、傾きの95%信頼区間は3.167, 6.063です。とりあえず勉強時間とテストの点数は正比例する、という事は言えそうですね。