こんにちは、小郷です。
ルイス・キャロル著「鏡の国のアリス」を読んだことはあるでしょうか。言わずと知れた「不思議の国のアリス」の続編小説です。
作中には赤の女王という人物が登場します。映画「アリス・イン・ワンダーランド」における強烈なビジュアルとキャラクターを覚えている方も多いかもしれません。

彼女が小説の中で発した有名なセリフがあります。
「It takes all the running you can do, to keep in the same place.(その場に留まるだけでも、全力で走らないといけないのよ)」
この言葉は、常に変わり続ける世界を生きる我々にとって、耳の痛い真実でもあります。
AIの登場によりホワイトカラー職種が淘汰されるのではないか、軍拡競争に遅れた国は大国に蹂躙されるのではないか。
人類史の中でも最も平和と言われる今の時代でも、激しい競争は続いているのです。

進化生物学には、こうした現象を説明する「赤の女王仮説（Red Queen Hypothesis）」という概念があります。
これは、「ある種の適応や改善は、競争相手(他の種)よりも優位に立つためであるが、相手もまた同様に改善し続けるため、生存のためにはデザインの継続的な改善が不可欠だ」とする仮説です。
つまり、進化とは絶対的な向上ではなく、相対的な優位性の維持のための終わりのない競争だという見方です。

目的とする環境、つまり「正解」が一意に定まっていると仮定しましょう。
このような環境下では、競争と淘汰を繰り返すことで、やがて他の種よりも最適に適応した最良の種が現れると考えることができます。
もちろん、現実の自然界ではそんな理想的な環境も、明確な「正解」も存在しません。進化とは、常に変化する環境との相互作用であり、絶え間ない相対的な適応の繰り返しです。

しかし、計算機の中で「目的関数」あるいは「評価基準」があらかじめ定義されている問題ならば、話は別です。ここでは、環境は静的で、ゴールも明確に定義されており、進化的探索が正解に向かって収束することが理論的に可能になります。
こうした発想のもと、生物進化の原理(突然変異・交叉・選択)を模倣して、ある問題に対して最適なパラメータを見つけ出す方法が、遺伝的アルゴリズム(Genetic Algorithm, GA)なのです。

ざっくりしたフロー

ざっくりとした処理フローは以下です。基本的には集団の中で優れた個体を選んで次世代に受け継がせることを繰り返すと、世代を経るに応じて改善していくと考えられます。その結果として最良の個体を生み出すことを期待しています。
野菜や動物の品種改良やポケモンの個体値厳選のようなものをコンピュータ計算の中でのみで実施するイメージです。

用語について、以下に詳しく解説していきます。

関連用語

個体（Individual）

生物学では「個体」はそのまま、集団内でそれぞれ独立した存在を指します。GAにおいても、個体は1つの「解の候補」です。
問題を解くための答えの候補がたくさん集まり、世代を経てより良い答えを見つける──この流れを支える最小単位が「個体」です。
冒頭では種間の競争について触れましたが、遺伝的アルゴリズム（Genetic Algorithm, GA）では、主に個体間の競争を扱います。

遺伝子（Gene）

生物学では、遺伝子は性質や形質を決定する情報の最小単位です。GAでも同様で、個体を構成する最小の情報単位が遺伝子です。
たとえば数値最適化問題なら、「ある変数に割り当てられた値」が1つの遺伝子に相当します。ある・なしの二値を扱うような問題であれば、各遺伝子は0または1という値を持ちます。

染色体（Chromosome）

染色体は、複数の遺伝子がまとまって構成される構造です。GAでも、染色体は個体の「設計図全体」を表します。我々ホモ・サピエンスは23対46本の染色体を持ちますが、GAではそれぞれの個体が持つ染色体は基本的には1本です(例外あり)。
実装上は、配列やビット列、リストなどのデータ構造として扱われます。染色体全体を操作することで、「突然変異」「交叉」などの進化的操作が可能になります。

遺伝子座（Gene Locus）

遺伝子座は、各遺伝子や遺伝子マーカーの染色体上の位置を表します。
GAでは、遺伝子座は「何の情報が何番目に入っているか」に対応します。つまり、変数Aの値は1番目の遺伝子座、変数Bは2番目……というように、情報の構造を決定する役割を持ちます。

ここまでを図にすると以下のような感じです。

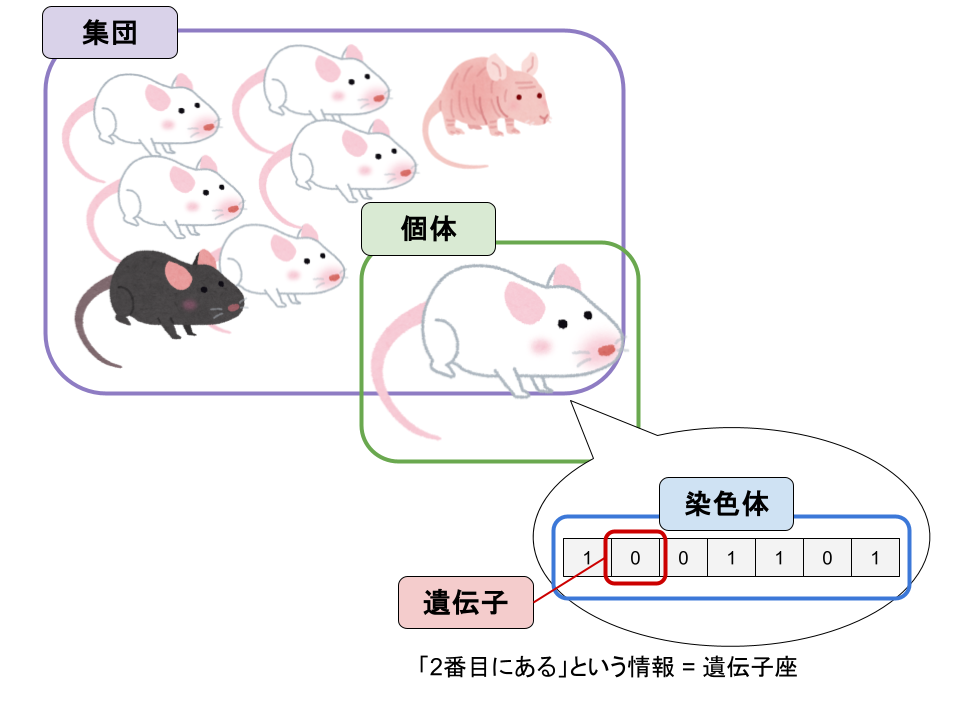
表現型（Phenotype）

表現型は遺伝子を元にして表面に出てきている特徴を指します。N番目の遺伝子の値が0だから身体が大きい、M番目の遺伝子の値が1だから体色が黒っぽい、などです。この表現型は、子孫の残しやすさに関係します。例えばモテるとか、食べられにくい、という差が個体間に現れます。
GAでは、各遺伝子の値を解釈（デコード）することで、解の候補がどのような特徴を持つか──つまり表現型（Phenotype）が得られます。

たとえばGAの最も基本的な応用例の1つに、「ナップザック問題」があります（後ほど詳しく解説します）。これは、N種類の品物をそれぞれ0個または1個ナップザックに詰めるとき、どのように詰めれば「重くならず」「価値が高くなるか」という最適な組み合わせを探す問題です。
ここでの「どの商品を選ぶか（0か1か）」という情報は、遺伝子型（Genotype）です。
これに対して、それぞれの品物の重量や価値の情報を参照して、選ばれた品物の合計重さや合計価値を計算したものが、表現型にあたります。

適応度（Fitness）

適応度はその個体が次の世代に遺伝子を残す量を表します。つまり、その環境に対してどれだけ適応しているかを表す指標です。例えばネズミならすばしっこくて的に捕まらず、餌をたくさん見つけられる個体が繁殖しやすくなります。
GAにおいて適応度（Fitness）は、ある個体（＝解の候補）がどれだけ問題に「適合」しているか、つまり目的関数に対してどれだけ良い結果を出しているかを数値で表したものです。たとえばナップザック問題であれば「合計価値」、巡回セールスマン問題であれば「総移動距離」などがそれに該当します。
適応度は、この目的関数の値そのもの、あるいはそれに変換を加えた数値（例：最小化問題で負に変換する）として定義され、進化の選択圧を決定します。この辺りは後の選択の項目で触れます。

選択・交叉・突然変異

選択（Selection）

生物における自然選択

ダーウィンの進化論においては、「最も強いものが生き残るのではなく、最も適応したものが生き残る」とされます。
例えば、捕食者に見つかりにくい体色を持つ個体、病気に強い個体、繁殖相手に好まれる個体などは、高い適応度を持ち、より多くの子孫を残す傾向があります。

GAにおける選択

GAでも、適応度の高い個体ほど次世代への寄与（＝子の生成に使われる確率）が高くなります。
ただし、適応度が低い個体もわずかに選ばれることがあり、探索の多様性を確保する工夫がされています。　なお、生物とは異なり雌雄の概念がないため、全ての個体は他の全ての個体と交叉する可能性があります。

代表的な選択方式

以下に一覧化しました。

それぞれの詳細は以下です。

ルーレット選択

• 個体の適応度に比例して選ばれる確率が決まる方式。
• 視覚的には「適応度の高い個体ほど大きな面積のスロットを持ったルーレットを回す」イメージ。
• 短所：極端な適応度の差があると、早期収束しやすい。

トーナメント選択

• ランダムに選んだ個体群から、最も適応度の高いものを選ぶ方式。
• トーナメントのサイズを調整することで、選択圧を調整できる。
• 計算が速く、実装も容易。

ランク選択

• 適応度の値そのものではなく、順位に基づいて選択確率を決める。
• 極端な適応度の差を抑えることで、多様性を維持しやすい。

エリート選択

• 最も適応度の高い個体をそのまま次世代にコピーする戦略。
• 優れた解が淘汰によって失われるのを防ぐ。
• 他の選択方式と併用されることが多い。

共通の考えとして、適応度が高いものほど次世代に遺伝子型が残りやすくなります。

交叉（Crossover）

ここからは親を選択した後の処理です。
交叉とは、二つの親個体の情報を組み合わせて、新たな子個体を生成する操作です。

自然界では

親の染色体が組み換えられることで、子に多様な特徴が現れます。ヒトをはじめとする多くの生物では、精子と卵子が作られる際に、対となる染色体が一部交換(組み替え)されます。この過程によって、自身のコピーではない、祖父母から受け継いだ形質が混ざり合った染色体が作成されることで、遺伝的多様性が生まれます。

GAでは

2個体、つまり両親の情報が混ざり合って新たな遺伝型を生成するという点で、生物学における文脈とは異なります。これは、親の良い特徴をうまく引き継ぎ、さらに良いこどもを作ることを目的にしています。

交叉の方法はいくつか存在しています。以下に代表的な三つの交叉の手法を示します。

それぞれの手法とメリット、デメリットは以下です。いずれの場合も、交叉しすぎると良い構造が壊れてしまうことがあるため、交叉率は試しながら調整することが重要です。交叉は、新しい可能性を試す操作です。

• 一点交叉
  • メリット: 親の構造をある程度維持
  • デメリット: バラエティは低くなりがち
• 二点交叉
  • メリット: 一点よりも多くの情報をミックスできる
  • デメリット: 交叉位置の選び方に依存する
• 一様交叉
  • メリット: 高い多様性を生み出す
  • デメリット: 構造が崩れやすい

多様性と構造の維持は、トレードオフの関係にあるわけですね。
勘の良い方はお気づきかもしれませんが、遺伝子の並び順の設計により、収束を早めることができる可能性があります。

突然変異（Mutation）

自然界では

突然変異とは、自然界では遺伝子を構成するDNA配列の一部（アデニン、グアニン、チミン、シトシン）が、他の塩基に置き換わる（点突然変異）ことで生じる遺伝情報の変化です。
これにより、遺伝子の働きが変化することがあります。

• 有益な突然変異：環境への適応を高める可能性がある（例：抗生物質への耐性）
• 中立的な突然変異：表現型に影響を及ぼさない
• 有害な突然変異：機能を損ない、疾患や生存率の低下につながることもある

親に起こった突然変異が生殖細胞に起こると、子に遺伝する可能性があり、有利な変異は世代を経て集団に広がることもあります（＝固定）。一方で、致死的な変異は淘汰により消滅します。

GAでは

GAでは、突然変異は探索空間の多様性を維持し、局所最適解に陥ることを防ぐための戦略的な操作です。主に、個体の染色体（ビット列や数値列）を構成する遺伝子の値を確率的に変更します。

• ビット列であれば 0 → 1 または 1 → 0
• 整数であれば、別の整数に置き換える
• 実数であれば、ランダムなノイズや変動値を加える（例：±0.01）

突然変異の目的は、交叉だけでは得られない多様性を導入することです。また、既存の解では到達できない、遠く離れた良い解へジャンプする可能性を作ることができ、局所最適解から脱出できる可能性があります。また、あえてノイズを入れることで、過剰な収束を防ぐこともできます。

ただし、突然変異の確率は調整が必要です。

• 高すぎる場合：進化ではなくランダム探索になる
• 低すぎる場合：局所最適に固着する

こうして選定された個体が、次の世代として用いられるわけですね。

ここまででようやく基本的な用語の説明は終わりです。
次は、「ナップザック問題」を例にして具体的なロジックの説明に進みます。

ナップザック問題

お金持ちの館に侵入した怪盗を想定してみましょう。
以下の条件があります。

• 目の前のお宝は選び放題です。お宝の重さや値段は様々です。
• 持って逃げられる総重量の限界が決まっているので、全ては持ち帰れません。

つまり、何を盗んで逃げるかを選ばなくてはならず、その制約の中でできるだけ稼ぎを多くしたいわけですね。こんな時に使えるのが最適化問題です。

お宝の種類は以下のように定義します。
現実の相場を考えたらどう考えても金が一番コスパがいいのですが(1g = 1.7万円くらい・執筆時点)、あくまで計算のための定義とお考えください。

遺伝子座	アイテム	価格（円）	重さ（kg）	コスパ（円/kg）
1	金の延べ棒	500,000	10	50,000
2	ダイヤの指輪	300,000	1	300,000
3	古文書の巻物	120,000	3	40,000
4	ガラスの帆船模型	200,000	4	50,000
5	札束	150,000	5	30,000
6	小型金貨セット	100,000	2	50,000
7	アンティーク懐中時計	180,000	2	90,000
8	宝石のペンダント	250,000	1.5	約166,667

制約は以下とします。

• 怪盗が一度に運べるのは10kgまでとします。
• それぞれのお宝は一つずつ存在しています(ダイヤの指輪10個という選択はできません)。

解候補は以下のように与えられます。今回はそれぞれのお宝を盗むか(1)、盗まないか(0)で各遺伝子座の値が決まるため、タプル列で値を持ちます。

$$ 解候補A = (0, 1, 0, 0, 1, 0, 0, 1) $$

この解に対する適応度を算出すると、2番目と5番目と8番目のお宝を盗んでいるので、以下のようになります。悪くはないですが、もっと盗めそうですね。

• 価格: 70万円
• 重量: 7.5kg

では高そうな模型帆船も盗んでみましょう。

$$ 解候補B = (0, 1, 0, 1, 1, 0, 0, 1) $$

• 価格: 90万円
• 重量: 11.5kg

残念。容量を超えてしまいました。この場合の評価方法は2種類あります。

1. 厳格な制約モデル: 10kgを超過した場合、適応度は0になる
   • メリット
     • 問題設定に対してシンプルで明快
     • 解が制約内に収まるかでフィルタされるため、探索空間が絞られる
   • デメリット
     • 初期条件や突然変異によってほとんどの個体が制約違反になると、全員のスコアが0になる。
     • 問題サイズが大きくなると、有効個体が激減しがち
2. ペナルティ付きモデル: 10kgを超過した場合でも、ペナルティを加えて得点を与える
   • メリット
     • 多様な個体が探索され、よりスムーズに有効解に近づく
     • 初期集団や突然変異による制約違反個体にも、情報価値がある
   • デメリット
     • ペナルティ係数のチューニングが必要
     • 非可能解が最後まで残ってしまうリスクがある

先に挙げた以外にも、無数の解の候補が存在します。これらの候補の選択と交叉を繰り返すことで、最適解を探すわけですね。

以下にPythonでの実装例を示します。

• 初期の個体数:：100
• 選択方法：ルーレット
• 交叉方法：一様交叉
• 交叉率：80%
• 突然変異率：1%
• 世代数：10
• 適応度の制約：10kgを超えたら0

import random

# --- パラメータ設定 ---
POP_SIZE       = 100    # 個体数
GENE_LENGTH    = 8      # 遺伝子長（お宝の種類数）
MAX_WEIGHT     = 10.0   # ナップザック容量（kg）
GENERATIONS    = 10     # 世代数

# 重さと価格のリスト（番号1〜8に対応）
weights = [10, 1, 3, 4, 5, 2, 2, 1.5]
values  = [500000, 300000, 120000, 200000, 150000, 100000, 180000, 250000]

# GAパラメータ（デフォルト値）
CROSSOVER_RATE = 0.8    # 一様交叉率 80%
MUTATION_RATE  = 0.01   # 突然変異率 1%

# --- 適応度関数（厳格モデル） ---
def fitness(individual):
    total_w = sum(w for g, w in zip(individual, weights) if g == 1)
    total_v = sum(v for g, v in zip(individual, values)  if g == 1)
    return total_v if total_w <= MAX_WEIGHT else 0

# --- 初期集団の生成 ---
def init_population():
    return [
        [random.randint(0, 1) for _ in range(GENE_LENGTH)]
        for _ in range(POP_SIZE)
    ]

# --- ルーレット選択 ---
def roulette_selection(population, fitnesses):
    total_f = sum(fitnesses)
    if total_f == 0:
        return random.choice(population)
    pick = random.uniform(0, total_f)
    current = 0
    for ind, f in zip(population, fitnesses):
        current += f
        if current >= pick:
            return ind

# --- 交叉（シングルポイント） ---
def crossover(p1, p2):
    if random.random() < CROSSOVER_RATE:
        point = random.randint(1, GENE_LENGTH - 1)
        c1 = p1[:point] + p2[point:]
        c2 = p2[:point] + p1[point:]
    else:
        c1, c2 = p1.copy(), p2.copy()
    return c1, c2

# --- 突然変異（ビット反転） ---
def mutate(ind):
    return [
        gene ^ 1 if random.random() < MUTATION_RATE else gene
        for gene in ind
    ]

# --- GAメインループ（10世代） ---
population = init_population()
fitnesses = [fitness(ind) for ind in population]

for gen in range(1, GENERATIONS + 1):
    new_population = []
    while len(new_population) < POP_SIZE:
        p1 = roulette_selection(population, fitnesses)
        p2 = roulette_selection(population, fitnesses)
        c1, c2 = crossover(p1, p2)
        new_population.append(mutate(c1))
        if len(new_population) < POP_SIZE:
            new_population.append(mutate(c2))
    population = new_population
    fitnesses = [fitness(ind) for ind in population]
    best_idx = fitnesses.index(max(fitnesses))
    print(f"Generation {gen:02d}: Best fitness = {fitnesses[best_idx]}")

# --- 最終結果 ---
best_idx = fitnesses.index(max(fitnesses))
print("\n最良解:", population[best_idx], "適応度:", fitnesses[best_idx])

手元で実行してみたところ、以下の結果を得ました。

最良解: [0, 1, 1, 0, 0, 1, 1, 1] 適応度: 950000

最初に私が適当に提示した解Aよりは、適応度が高くなっています。

解は一つとは限らない

ホモ・サピエンスにおける例を一つ示しましょう。
鎌形赤血球症という遺伝病が知られており、これは赤血球がわらび餅を潰したような形状ではなく、柿ピーのような形状になることで、うまく酸素を取り込めないことにより貧血症状を呈するものです。通常の環境では、この形状は酸素運搬能力を低下させるため、適応度は低いと考えられます。実際に、重症型ホモ接合体の平均寿命は60歳程度になるようです。

ところが、マラリアが流行している地域では話が違ってきます。
マラリア原虫（Plasmodium属）は、ヒトの赤血球に侵入して増殖しますが、鎌形赤血球を持つ人の細胞内では増殖しにくいことが知られています。特に、ヘテロ接合体（正常な遺伝子と異常な遺伝子を1つずつ持つ場合）では、貧血症状は出にくい一方、マラリアへの抵抗性が高くなるという進化的なトレードオフが存在します。

このように、「どの表現型が高い適応度を持つか」は、環境に依存して変わり得るのです。
GAでもこれは同様で、評価関数（フィットネス関数）や制約条件が変われば、「優れた個体」の定義そのものが変化します。
つまり、「良い解」とは絶対的なものではなく、問いや環境＝問題設定に応じて相対的に決まるのです。

とはいえ、限定的な環境に対して最適になると、局所適合という問題が発生します。マラリアの流行しない地域においては、鎌形赤血球症の遺伝子変異はむしろマイナスとなり得えます。
このように、GAによって得られた解が本当に最適であるかどうかは、常に問題設定や環境条件を踏まえて再評価する必要があるのです。

おわりに

本記事では、生物学の「個体」「遺伝子」「染色体」「表現型」「適応度」といった概念の解説とともに、ナップザック問題を題材にした遺伝的アルゴリズム（GA）の基本的な仕組みを解説しました。
解の表現から適応度の設計、ルーレット選択、交叉、突然変異まで一通りの流れを追うことで、GAがどのようにして「ランダム探索」と「解の活用」を両立し、最適解に近づくのかをイメージしていただけたかと思います。

なお、本稿で解説した最適化手法を現実の人間社会に当てはめると、それはまさに「優生学」の領域に踏み込むことを意味します。歴史が示すように、優生学は人権侵害と悲劇を招いた大きな過ちでした。私たちはその失敗から学び、遺伝的アルゴリズムをはじめとする最適化技術を、あくまで「問題解決のツール」として節度をもって利用すべきでしょう。

また、別の文脈では、旧ソ連のトロフィム・ルイセンコの一派は「環境に適応した作物を選び抜けば、理想の農業が実現できる」と信じてミチューリン農法と呼ばれる農法を実施しました。日本にはヤロビ農法として広まった時期もあります。
生物の進化＝環境適応という(社会主義・共産主義にとって都合の良かった)一面を信奉しすぎた結果、遺伝学の否定と農業の壊滅を招いたという意味で、最適化の暴走が引き起こした悲劇的実例とも言えるでしょう。
ちなみに遺伝的になんの意味もないというわけではなく、遺伝子配列に変化はないものの、一代限りで遺伝子の発現の調整が行われる、エピジェネティクスの領域に片足を突っ込んでいたという、成果らしきものは存在します。どちらかというとこちらは分子生物学の領域になりますが。

このように遺伝的アルゴリズムの元になった進化学や集団遺伝学には面白い逸話がたくさんあります。
……が、その話はまた別の機会にするとしましょう。