こんにちは、小郷です。
曖昧な中でベストを求めたい、試しながら決めたい、という場面はビジネスに限らず、日常生活の中にもありうると思います。判断材料はあるけど、どうしたらいいかわからない…という状況に光を照らしてくれるのが「ベイズ」です。本記事では身近な活用例とともに、中身について解説していきます。
概念としては「なんとなくの確率に対して後から情報を足していって、それっぽい答えに近づける」ものです。
ベイズの歴史
その歴史は古く、18世紀中頃にまで遡ります。これは回帰の概念よりも古いものとなります。
牧師にして数学者であったトーマス・ベイズにより「未知の確率に関する確率」に対する理論が整えられました。その後、19世紀に入ってからラプラスの魔で有名なピエール=シモン・ラプラスにより「確率更新の一般的な手法」としてベイズの定理を体系化します。
20世紀に入ると、フィッシャー、ネイマン、ピアソンらが「頻度主義統計(頻度論)」を構築しました。頻度論では「確率とは繰り返し観測によって安定して現れる比率そのものである(客観確率)」と考えるため、「確率を未知の変数として扱って推定する」「確率とは知識や信念の度合い(主観確率)」というベイズの立場は否定します。特に20世紀前半は頻度論が主流となり、ベイズは忘れ去られました。
しかし、マシンパワーの発展や、不確実性を扱える点が現代のニーズとマッチしたことから、ベイズは再び復権しました。
現在はベイズも主観と客観に分類されることがあり、主観ベイズでは「この業界ではこうだから」を容認し、客観ベイズでは「できるだけ人間のバイアスを排除し、誰がやっても同じ事前確率を使う」という考え方でデータを扱います。
ビジネスの現場では、主観と客観が織り交ぜられることがあるでしょう。例えばサンプル数が少ない場合など。
ベイズが使われる場面
よく例として挙げられるのは、スパムメールの判定です。
つい最近、某証券会社を騙るフィッシング詐欺の事例があったことは記憶に新しいですね。
スパムメール判定
例えば、以下のようなフレーズが入ったメールが届いたことはありませんか?
- あなたのアカウントに問題があります
- 支払いに問題があります
- 確認のためこちらをクリックしてください
- 24時間以内に対応が必要です
- A○azon/楽○/○井○友など実際の企業名
典型的なフィッシング詐欺のメールの文面の一部です。
これで案内に進んでしまったらご愁傷様。
アカウント情報やキャッシュカード情報などを盗み取られて悪用されることでしょう。
我々人間は、こうした文面を「怪しい」と直感で判断できます。
しかし、世界中のメールをすべて人間が目視チェックするわけにはいきません。
そこで登場するのが、迷惑メールを自動で判定・振り分けるフィルター機能。
多くのメールクライアントには、こうした機能が初めから実装されています。
その判定ロジックはシンプル。
特定の単語やフレーズの出現頻度から「スパムである確率」を推定し、一定の閾値を超えたら迷惑メールと判断する。つまり、確率で判断しているわけです。
ここで使われているのがナイーブベイズ分類器です。
ここでナイーブとは、「それぞれの変数が独立である」などの現実では必ずしも成り立たない単純な仮定に立つ手法を意味します。単純であるが故に計算が早く、実用的なモデルといえます。
ベイズの公式
まずは最も基本的なベイズの公式を以下に示します。
$$ P(A \mid B) = \frac{P(B \mid A) \cdot P(A)}{P(B)} $$
各変数は以下の意味を持ちます。
- \(P(A \mid B)\) : Bが発生した時、Aである確率(事後確率)
- \(P(B \mid A)\) : Aが発生した時、Bも発生する確率(尤度)
- \(P(A)\) : Aが発生する確率(事前確率)
- \(P(B)\) : Bが発生する確率(正規化定数)
スパムメール判定の文脈では以下に言い換えることができます。
- \(P(A \mid B)\) : ある文言が含まれている時、そのメールがスパムである確率(=知りたい値)
- \(P(B \mid A)\) : スパムメールにこの文言が含まれている確率
- \(P(A)\) : メール全体のスパムである確率
- \(P(B)\) : メール全体である文言が入っている確率
\(P(B \mid A)\)、\(P(A)\)、\(P(B)\)は経験則、つまり既存のスパムメールの観測データから求めることができます。仮に、100万件のメールを集めたとき、以下のような結果が得られたとしましょう。
- スパムメールが40万件: \(P(A) = \frac{400,000}{1,000,000} = 0.4\)
- スパムかつ、「あなたのアカウントに問題があります」という文言が含まれる3万件: \(P(B \mid A) = \frac{30,000}{400,000} = 0.075\)
- すべてのメールの中で「あなたのアカウントに問題があります」という文言が含まれる4万件: \(P(B) = \frac{40,000}{1,000,000} = 0.04\)
ここから公式に当てはめて計算すると「あなたのアカウントに問題があります」という文言が含まれているメールがスパムである確率は、先の条件では75%となります。
$$ P(A \mid B) = \frac{0.075 * 0.4}{0.04} = 0.75$$
このように、手元にある経験則、つまりデータから予測を立てることができます。
ベイズ更新
先に、ある一種類の文言が含まれるメールがスパムメールであるかの確率を求めました。
ベイズ更新という手順を用いれば、もう一つ文言を追加して、スパムメールであるかの確率を更新することができます。
ここでは以下の仮定を立ててみましょう。追加する文言は「24時間以内に対応が必要です」としてみましょう。
- \(P(A \mid B)\) : 「24時間以内に対応が必要です」と「あなたのアカウントに問題があります」の両方の文言が含まれているとき、そのメールがスパムである確率(知りたい値)
- \(P(B \mid A)\) : スパムメールに上記2つ文言が含まれている確率(40万件中2万件と仮定)
- \(P(A)\) : 「あなたのアカウントに問題があります」という文言が含まれるメールが、スパムである確率(前フェーズの事後確率、0.75)
- \(P(B)\) : メール全体で「24時間以内に対応が必要です」と「あなたのアカウントに問題があります」の両方が含まれる確率(100万件中4万件と仮定)
では計算してみましょう。
$$ P(A \mid B) = \frac{\frac{20,000}{400,000} * 0.75}{\frac{40,000}{1,000,000}} = 0.9375 $$
となり確率が更新され、上記の文言二つが含まれるメールは、より高い確率でスパムメールでありそうです。
\(P(A \mid B)\)が1を超えてしまう場合は、なんらか前提がおかしいので、元データを見直すなどしてみてください。
ベイズ推定とは
ベイズの定理では、あらかじめ分かっているパラメータを単なる確率として置きました。
一方でベイズ推定では、分布を前提に置いています。以下の式で表すことができます。
$$ P(\theta \mid D) = \frac{P(D \mid \theta)・P(\theta)}{P(D)} $$
- \(\theta\): 未知の確率変数であり、\(P(\theta)\)は事前分布と呼ばれる
- \(D\): 観測データであり、\(P(D)\)は観測データの集合である正規化定数、\(P(\theta \mid D)\)は事後分布として定義される
出力は不確実性付きの推定です。
例えば回帰分析などは、ある値Aの時にはある値Bが一つだけ決まる「点推定」です。入力が50ならば出力は100、というように一つの値が決まるのですが、現実には95だったり、105だったりするわけです。この曖昧さを許容し、入力を分布にすることによって出力も分布になり、出力を確率的に予測するのがベイズ推定です。
では「事前分布」とやらには、どのような決め方があるのでしょうか。\(P(\theta)\)に当たる部分ですね
まずは「どういう仮定・知識に基づいて分布を選ぶか」という視点で、以下のようなものがあります。
- 特定のパラメータを優先せず、情報が何もないから、全ての場合で同じ確率で起きてそう、というような一様分布を採用するなど、仮定をもとに決める。無情報事前分布と呼ばれる。
- 極端な値を避けて常識的な範囲にデータが収まるという前提に分布を決める。弱情報事前分布と呼ばれる。
- 大体こんな感じだよね、というある程度のドメイン知識があって、その事前分を採用する方法。経験事前分布と呼ばれる。
次に、「(主に計算上の都合で)どういう形の分布を使うか」という視点では以下のようなものがあります。
- 共役事前分布: 尤度関数と事前分布組み合わせによって、事後分布の形が変わらないので、計算が容易である。
- 非共役事前分布: 上記に当てはまらないもの。事前分布と事後分布の形が解析的に求められない。MCMCなど数値的手法を必要としている。
実際に計算してみる
コインの表裏を例に計算してみましょう。
未知のパラメータ\(\theta\)はコインが表を出す確率とします。この\(\theta\)を推定するために、事前分布、尤度、そして観測データを用いて事後分布を求めます。
1. 事前分布の設定
コインの裏表という2値が出る確率は経験的には均等ですが、ここでは無情報として\(\theta\)に対して一様とみなし、事前分布を一様分布(Beta分布の特殊ケース)で表現します。以下の設定では、\(\theta\)が0から1まで均等に分布していると仮定しています。
$$ P(\theta) = Beta(\theta ; \alpha = 1, \beta = 1) $$
2. 観測データの収集
実際にコインを投げた結果が観測データになります。10回行って、表が7回、裏が3回出たとします。
$$ D = \{表: 7回, 裏: 3回\} $$
ベイズの理解しづらいポイントとして、\(P(D)\)は単純に割合で求められないという点です。式で表すと以下のように定義されます。
$$ P(D) = \int P(D \mid \theta)P(\theta) d\theta $$
ここで、\(P(D \mid \theta)P(\theta)\)は\(\theta\)に依存する関数となるため、総和(=積分の結果)は1になりません。そうすると\(P(\theta \mid D)\)の総和が1ではなくなり、確率関数としては破綻します。確率関数として成り立たせるための定数が、\(P(D)\)の役割というわけです。一旦、次の計算では無視して良い値です。
3. 尤度の定義
コイン投げは独立な二項試行とみなせるので、表が出る回数は二項分布に従います。尤度関数は以下のように定義できます。
$$ P(D \mid \theta) = \begin{pmatrix} 10 \\ 7 \end{pmatrix} \theta^7 (1 – \theta)^3 $$
4. 事後分布の計算
先に述べた通り、分布\(P(D)\)は正規化定数であり、\(\theta\)に依存しないため、\(\theta\)に関する形としては以下のように表現できます。\(\propto\)は比例するという意味です。
$$ P(\theta \mid D) \propto P(D \mid \theta)P(\theta) $$
\(P(\theta)\)は一様分布と仮定しているので、\(P(\theta) \propto \theta^{1-1}(1 – \theta)^{1-1} = 1\)と表されます。つまり、事後分布は以下の形式で表されます。
$$ P(\theta \mid D) \propto \theta^7(1 – \theta)^3 $$
この形式はbeta分布の形式に一致します。
$$ Beta(\theta; \alpha, \beta) \propto \theta^{\alpha – 1}(1 – \theta)^{\beta – 1} $$
beta分布の一般式は以下のように定義されています。
$$ Beta(x; \alpha, \beta) = \frac{x^{\alpha – 1}(1 – x)^{\beta – 1}}{B(\alpha, \beta)} $$
先の事後分布の式に当てはめると、\(alpha = 8\)、\(beta = 3\)とそれぞれ求めることができます。
$$ P(\theta \mid D) = Beta(\theta; \alpha = 8, \beta = 4) $$
5. 期待値の計算
Beta分布の平均は以下で求められます。
$$ E[\theta \mid D] = \frac{\alpha}{\alpha + \beta} = \frac{8}{8 + 4} \approx 0.67 $$
したがって、今回の試行からはコインが表になる確率の推定値は約67%であることがわかりました。
今回求められた分布を可視化すると以下のようになります。
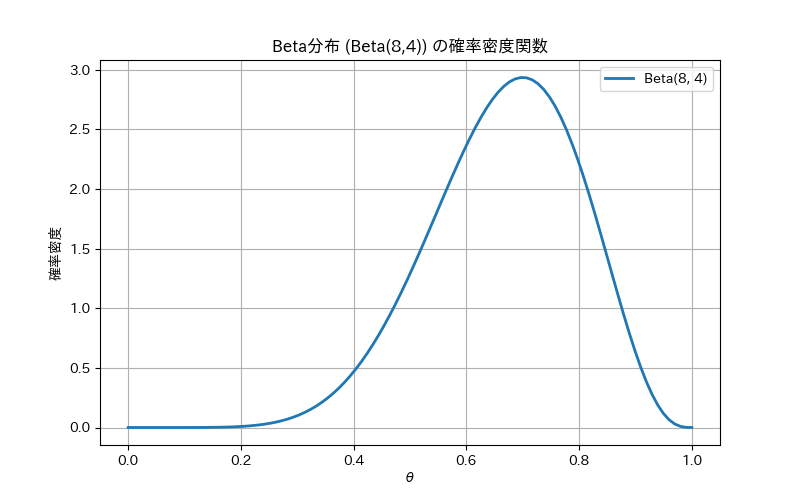
さらに正確にしていきたい場合、追加の試行をしたくなると思います。
その場合は、先の事前確率にBeta(8,4)を置いてあげましょう。
おわりに
今回の記事ではベイズのさわりの部分だけ解説しましたが、さらに掘り下げようとすると書籍が一冊できてしまうので、その部分は市販の解説書に任せたいと思います。
ただ、いくら曖昧な状態からもある程度正しい値を推定できるからといって、最終的に判断を下すのは人間です。推定はあくまでも推定でしかないので、盲信してはいけないのは、昨今のAIと同様です。
統計的な結果とは適度に距離を保ちつつ、判断基準の一つとして考えるのが良いでしょう。
例えば投資先の決定を推定で実施していたプログラムは、きっと今回のトランプ・ショックの予想はできなかったことでしょう。ある程度相場は下がっていて、下落推移が見えていたとしても、さすがにあのような雑な計算で出した高関税になるなんて、当事者しか予想していなかったでしょう。その後の株価の大暴落は、当事者たちでさえも。