こんにちは、小郷です。
今回はゲーム理論のほんの一部について解説します。
この世界のあらゆる場面で、複数のプレイヤーがいる時に協力や競争が発生します。
例えば会社内では、周りの同僚は同じ目標に向かう仲間でありながら、出世競争のライバルでもあります。
会社間では、やはり同じ目標に向かいながら協力することもあれば、激しい売上競争が発生することもあります。
この競争をするとき、どのように行動すべきかヒントを与えてくれるのがゲーム理論です。
協力と裏切りの発生には、常に利益構造が関係します。
現生人類が生存競争を勝ち抜くことができた要因の一つは、ネアンデルタール人よりも個体間で協力的だったためと考えられていますが、協力は決して我々だけの特権ではありません。
この仕組みは、生き物全体に共通して見られる行動様式です。
最初のセクションでは、自然界における具体例を見てみましょう。
コウモリの協力関係
ナミチスイコウモリでは、餌を取れなかった仲間に餌を分け与える現象が知られています。このような行動は利他行動として知られています。
自身の餌を与えた場合、自身はその分お腹を空かせ、かつ危険を犯して餌を取りに行く必要があるため、超短期的にはインセンティブがありません。
彼らの食事はその名の通り血ですので、牛や馬、稀ではありますが人間の血を吸います。
体の小さな彼らが巣穴から抜け出して大型動物の血を吸うことは、それだけで高いリスクを孕んでいます。
しかし餌の供与の関係は相互的で、ある個体が与えるシチュエーションもあれば、与えてもらうシチュエーションもあります。
以下のメカニズムが働いていると考えられています。
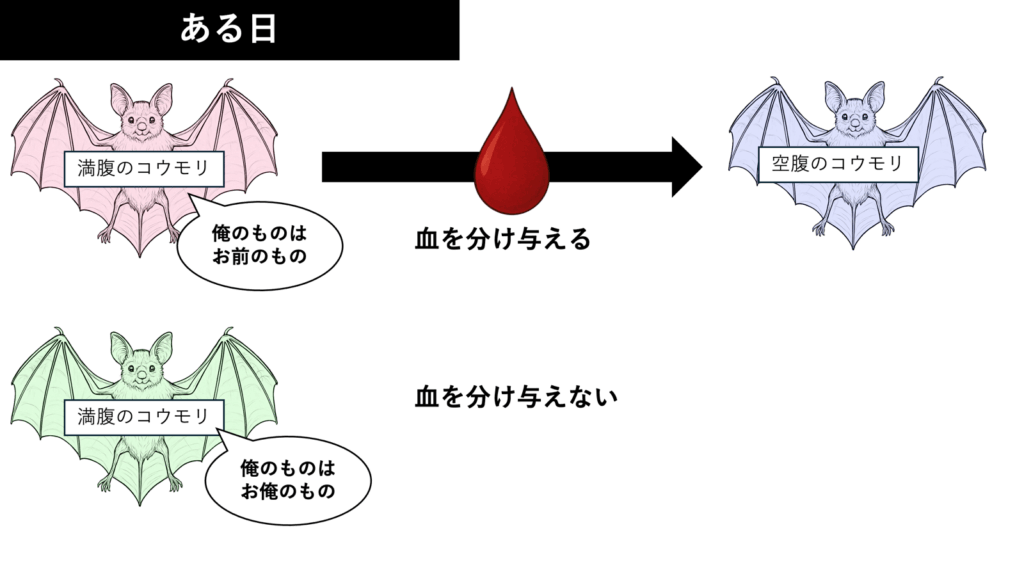
仲間を助けると自分も助かる
満腹時に他の個体に餌を与えた個体は、与えなかった個体より、自身が空腹の時に貰える餌の量が多かったことが確認されています。
これは与えないが貰うだけ、というフリーライダー(=裏切り)の排除機構として働きます。

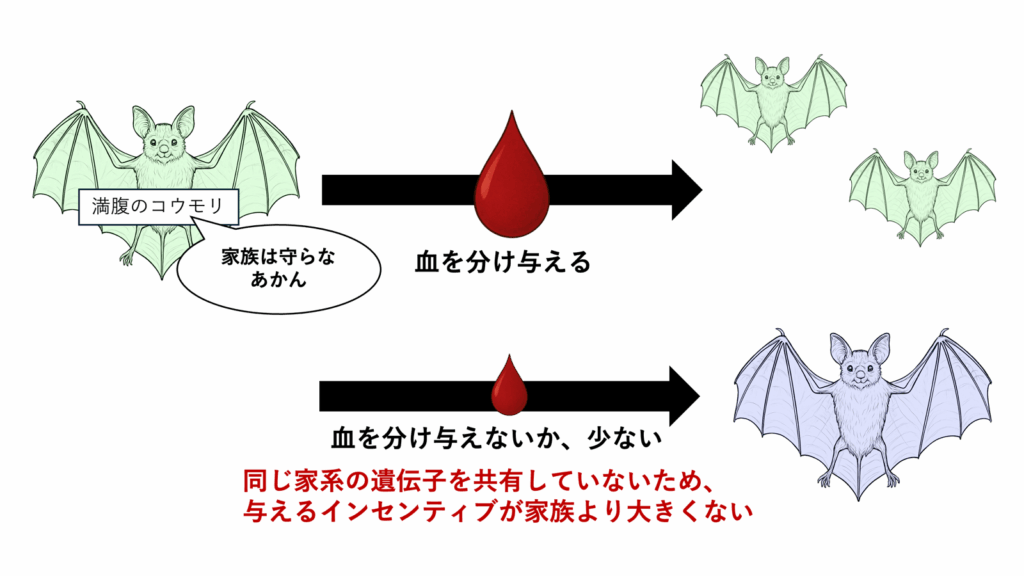
「家族は助け合うもの」は遺伝学で説明できる
血縁関係にあるほど、餌の供与の確率が高まることが確認されています。
これは自身と遺伝子が近い個体の生存率を上げることで、自身の遺伝子を残りやすくする目的があります。
このあたりはハミルトンの血縁淘汰説で説明されています。
上記の通り、情緒ではなく将来の利益=インセンティブを期待して、彼らは餌のシェアを行います。
餌を与えることで、自身の生存率、あるいは集団内における遺伝子のシェアを上げることができるのです。
このような利益のやり取りがどのように安定し、なぜ裏切りではなく協力が選ばれるのか。
その仕組みは、ゲーム理論によって明確に説明できます。
ゲーム理論基礎
ゲーム理論とは、複数の意思決定者がいて、互いの行動が結果に影響を及ぼしあう状況を、数学でモデル化して分析する学問です。
数学者であるジョン・フォン・ノイマンと、経済学者であるオスカー・モルゲンシュテルンによって基本的な理論が構築されました。
統計や機械学習、一般的な最適化は「自分の目的関数をどう最適化するか」が焦点になっています。
しかしゲーム理論では、自分以外のプレイヤーが存在しています。
- 自分がどう動くか
- 他者がどう動くか
- その相互作用で何が起きるか
これらの相互依存によって、シンプルな最適化だけで行動を決めることは難しくなります。
ゲーム理論の基本要素
ゲーム理論はどんな複雑な現象も、以下の3つに分解します。
- プレイヤー
ゲームの参加者を指します。生物の個体でも、会社でも、とにかく何らかの選択をする存在です。 - 戦略
プレイヤーが取りうる選択肢です。
「協力/裏切り」「値上げ/値下げ」「餌を与える/与えない」などを指します。 - 利得
選択の結果から生じる利益または損失です。
「生存率」「評判」「売上」などを指します。
広義では上記にゲームのルールを加えた4要素とする場合もあります。
ゲームの分類
ゲームはいくつかの軸で分類することができます。
プレイヤー同士の対立構造による分類
- 協力ゲーム: プレイヤー同士が協力する圧力がかかるゲームで、合意すると全体が得られる特典が増えます。
例: カルテル・国際交渉 - 非協力ゲーム: 各プレイヤーは独立して意思決定し、合意はできません。
例: 囚人のジレンマ・価格競争・核抑止戦略
以下はカルテルと、その裏切りの例です(協力ゲーム)。
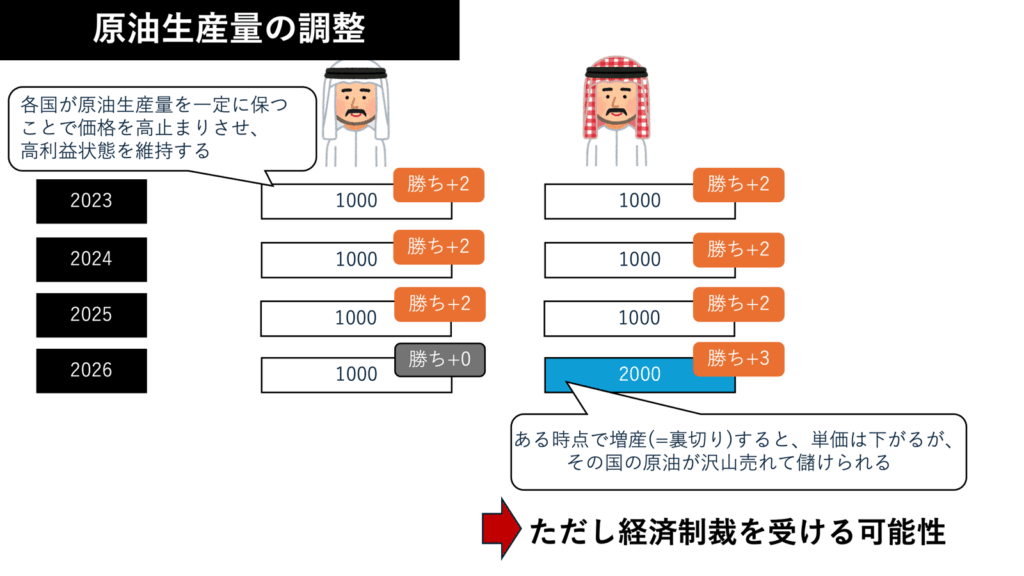
全体の得点合計による分類
- ゼロサム・ゲーム: 誰かの利益は必ず他者の損失になるゲームで、全体の得点合計は0となります。
例: 野球などスポーツのリーグ戦 - 非ゼロサムゲーム: 協力すれば双方得をする余地があります。
例: 鹿撃ちゲーム・生物の利他行動・社会活動・囚人のジレンマ
以下はゼロサムゲームの例です。なんでや阪神関係ないやろ
非ゼロサムゲームの代表例である囚人のジレンマは後ほど詳しく触れます。
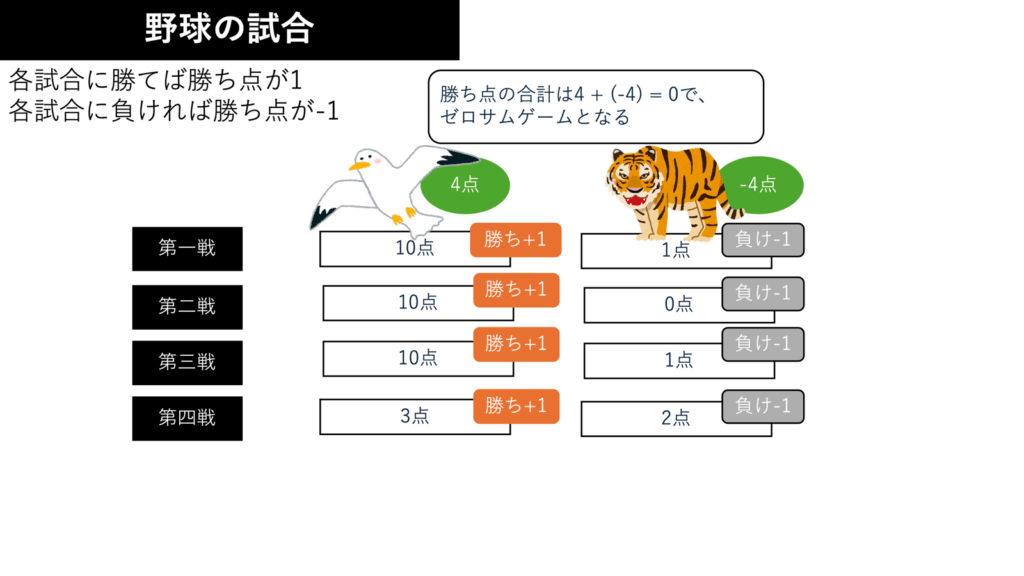
選択のタイミングによる分類
- 同時ゲーム: 各プレイヤーは同時に選択を行い、相手が何を選択したかは自分の選択を明らかにするまでわかりません。
例: じゃんけん・囚人のジレンマ・ポ◯モン対戦 - 逐次ゲーム: 各プレイヤーは相手の選択を見てから戦略を決めることができます。
例: 後出しじゃんけん・チェス・将棋・遊◯王などのターン制カードゲーム
情報公開領域の違いによる分類
- 完全情報ゲーム: 全てのプレイヤーの行動が公開され、隠れた情報がないゲームです。
例: チェス・将棋・囲碁 - 不完全情報ゲーム: 相手の意図や戦略が部分的に不明であったり、相手の選択の理由が公開領域にないゲームです。
例: ポーカー・オークション・価格競争
実行回数による分類
こちらの分類による選択の違いは、後ほど詳しく解説します。
- 単発ゲーム: 1回の選択だけで最終得点を決めるゲーム。
- 繰り返しゲーム: 複数回のセッションの合計得点で、最終得点を決めるゲーム。
このセクションでは、ゲーム理論の基本的な情報を説明しました。
次のセクションでは、囚人のジレンマを題材にどのような戦略が有効かを解説します。
囚人のジレンマの構造解説
協力と裏切りを考えるうえで、最も基本的でありながら奥深いモデルが「囚人のジレンマ」です。
単純な設定でありながら、なぜ協力が難しく、なぜ裏切りが合理的に見えてしまうのか――その数理構造を端的に示してくれます。
ゲームのルール

プレイヤーは 2人の囚人 です。なんらかの犯罪で共犯関係にあります。
2人の囚人は別々に尋問され、互いに連絡を取ることができません。
この状況では、相手がどのような選択をしたかを事前に知ることはできず、
ゲーム理論における 不完全情報ゲーム の典型例となります。
各プレイヤーの行動
2人の囚人は、それぞれ以下のいずれかを選択します。
相手の選択は自分の選択が確定するまで開示されず、
意思決定は同時に行われます(同時ゲーム)。
- 黙秘(協力):相手を裏切らず、自分の関与を認めない
- 自白(裏切り):相手を売り、自分だけ罪を軽くしようとする
利得(量刑)の決定
2人の選択の組み合わせに応じて、与えられる刑罰が変わります。
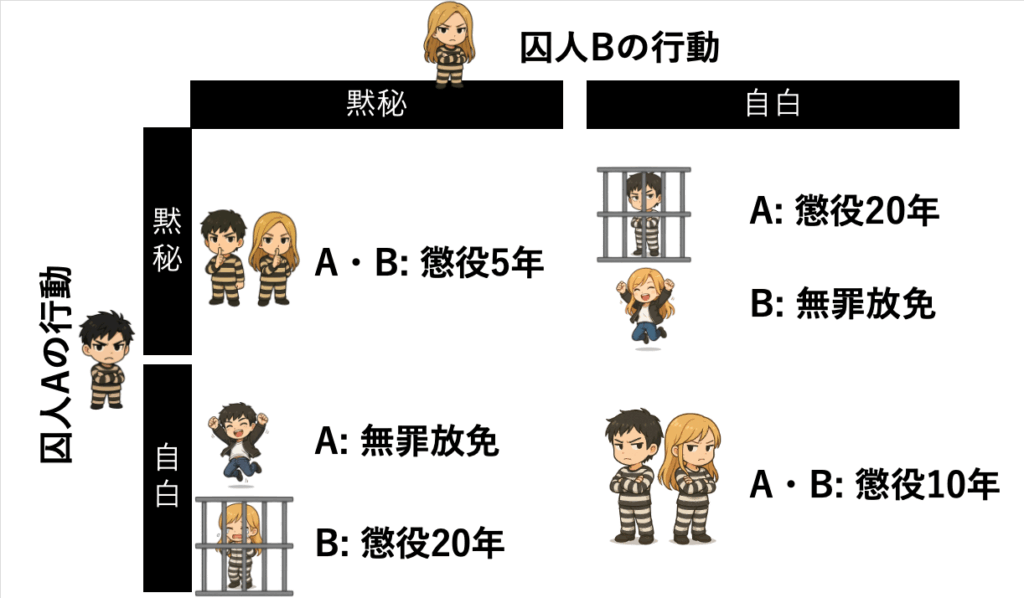
- 両方が黙秘(協力): 2人とも軽い罪
- 片方が自白(裏切り)、もう片方が黙秘(協力): 自白した側は無罪、黙秘した側は最も重い刑
- 両方が自白(裏切り): 2人とも中程度の刑
個々人の利益の量を以下と置くと、以下のようになります。
- T:自分だけ自白して相手を裏切ったときに得られる最大の利益
- R:互いに黙秘したときに得られる報酬
- P:互いに自白したときの罰
- S:自分だけ黙秘して裏切られたときの最悪の結果
この結果の大小関係は以下のように整理されます。
$$T > R > P > S$$
この構造が意味するもの
ジレンマとは、そう反する2つの選択肢の板挟みになり、
どちらを選んでも不利益が生じる可能性があり、態度を決められない状態を指します。
ここでは、
「各プレイヤーは自分にとって最も得な選択をしているが、
その合理的選択の積み重ねが全体の損失を招く」
ことを指します。
つまり、最適な個人行動が最適な集団行動と一致しない状態がジレンマの本質です。
囚人のジレンマは、この矛盾を最も単純な形で示したモデルであり、
協力・裏切りの理解につながる重要な基本構造となります。
囚人のジレンマにおける各プレイヤーの思考ロジック
ここからは、プレイヤーの視点で選択の試行過程を追っていきましょう。
■ ステップ1:相手が黙秘する場合を考える
もし相手が黙秘するとしたら、自分の選択は以下のように評価されます。
- 自分も黙秘: 懲役5年(軽い刑)
- 自分が自白: 無罪放免(最も得)
この状況では、自白のほうが黙秘よりも明確に有利です。
■ ステップ2:相手が自白する場合を考える
次に、相手が自白したとしたら、自分の選択は以下のように評価されます。
- 自分が黙秘: 懲役20年(最悪)
- 自分も自白: 懲役10年(まだマシ)
この状況でも、自白のほうが黙秘より損失が小さいくなります。
■ ステップ3:2つのケースを比較する
相手が黙秘しても自白が有利。相手が自白しても自白が有利。
つまり、自分の視点では自白(裏切り)はどんな状況でも最適な選択になります。
これは、支配戦略(ドミナント戦略)と呼ばれます。
なので、自白が唯一の合理的選択肢として浮かび上がります。
■ ステップ4:相手も同じ計算をする
囚人Aも囚人Bも、同じ条件で同じ推論を行います。
両者にとって自白が支配戦略である以上、合理的に考えれば両者とも 自白 を選ぶと考えられます。
しかし、両者が懲役10年となり、両者5年よりは悪い結果になります。
これは両者にとって非効率ですが、個別に合理的判断を積み重ねた結果、避けられない選択です。
このように、互いに自白する状態は「誰も自分だけ行動を変えても得にならない」ため、
ゲーム理論でいうナッシュ均衡となります。
ゲーム回数と戦略の違い
囚人のジレンマは、何回プレイするかによって戦略が全く変わります。
ゲーム回数は、次の3種類に分かれます。
1. 単発ゲーム: 協力は不可能
単発の施行では、先の理由で自白一択になります。
2. 有限回ゲーム: 協力は帰納的に崩壊する
回数がわかっていても、協力は不可能です。
後ろ側から考えたとき、
- 最終N回目: 1回ゲームなので裏切りが支配戦略となる。
- N-1回目: 最終回に裏切られることが確定しているため、裏切るしかない。
- …
- 1回目: 遡って全て裏切りが合理化される。
つまり、回数が有限であり、終わりが見えていると協力は崩壊します。
これは“最終手から逆にたどると、協力が論理的に成り立たない”という構造であり、
ゲーム理論では後ろ向き帰納法として知られています。
3. 無限回ゲーム/回数不明:協力が発生する唯一の条件
この場合に初めて協力が可能になります。
理由はシンプルで、裏切ると、未来の協力関係が壊れて長期的に損するためです。
その“未来の価値”を表すのが 割引率 \(δ\)。
協力が成立する条件は以下が成り立つ場合です。
$$ δ(R−P)≥T−R $$
- 今日裏切って一時的に得られる利益\((T − R)\)より
- 未来の協力が失われる損失\((δ(R − P))\)が大きいとき
協力が合理的になります。
割引率とは
割引率\(δ\)の意味をもう少し詳しく解説します。
無限回(あるいは回数がわからない)囚人のジレンマでは、
プレイヤーは「未来の利得をどれくらい重視するか」を考える必要があります。
この“未来の価値”を表すのが 割引率 \(δ\)(デルタ) で、0~1の範囲で決まります。
$$ 0<δ<1 $$
\(δ\)が1に近いほど、未来の利得を現在とほぼ同じ価値として扱います。
逆に、\(δ\)が小さいほど、未来を軽視します。
より平易な言葉で表すと、「相手が今後も協力してくれるだろう」という期待の強さを表す指標です。
囚人Aと囚人Bが恋人同士であれば、互いに協力を期待できるため、主観的な割引率 \(δ\) は高くなるでしょう。
逆に、闇バイトで集まったばかりの赤の他人であれば、未来の関係を重視する理由がほとんどなく、\(δ\) は低くなると考えられます。
これは吸血コウモリの例でも同様で、過去に血を与えてくれた個体に対しては「この相手は裏切りにくい」という期待が働くため、主観的な\(δ\) が高くなると解釈できます。
しかし、ゲームの回数が有限であり、終わりが見えている場合には、最終手に未来の価値が存在しないため、どれほど関係性が良くても \(δ\) は実質的に 0 に収束します。
繰り返しゲームで協力が維持される理由
割引率 \(δ\) が十分に高い場合、未来に得られる協力の利益が大きくなるため、
裏切りより協力を選ぶ方が合理的になります。
単発ゲームでは裏切りが最適でしたが、
繰り返しゲームでは裏切りが次回以降の協力を失わせるペナルティになります。
懲役5年をずっと続ける方が、懲役10年をずっと続けるよりマシであるからです。
さらに、繰り返しゲームでは 返報戦略(しっぺ返し戦略 など)が使用可能になり、
相手が協力すれば自分も協力し、裏切れば次のラウンドで報復することができます。
この仕組みによって、裏切りの魅力は大きく減少し、協力が自然に維持される構造が成立します。
繰り返しがあると、協力を壊したときの未来の損失が裏切りを抑制します。
逆に、未来が存在しない(δが低い)ときには協力は崩れます。
裏切り戦略
いつ裏切るか?
ここで注意したいのが、ずっと協力し続ける関係はナッシュ均衡と呼ばない点です。
いくら相手が協力を続けていても、自分だけ裏切った瞬間に最も大きな利得(T)を得られるため、
協力は均衡として安定していません。
つまり、協力は“揺らぎに弱い状態”なのです。
では、協力関係のなかに裏切りが差し込まれる瞬間はどこにあるのでしょうか。
1. 未来の価値が下がったとき(δの低下)
協力関係は、未来の利得をある程度重視しているときにのみ成立します。
しかし、
- 関係が終わりに近づく
- 相手が信用できない行動をとる
- 相手と再び会う確率が下がる
- 状況が不安定になる
などの要因で 割引率 δ が低下すると、協力の期待値が急落します。
δ が下がると、
「次回以降の協力への期待 < 今日裏切って得る利益」
となり、裏切りが合理的になります。
2. 協力のコストが急に上がったとき
協力のための負担(C)が大きくなると、
短期利得 T との差が広がり、裏切りが魅力的になります。
3. 相手の協力確率(p)の推定が変化したとき
協力は「相手が協力者である」という期待(p)があって初めて成り立ります。
しかし、
- 相手が裏切った
- 相手の態度が曖昧になった
- そもそも相手が信用できない
といった状況では p が下がる。
すると、
未来の協力期待値 \( δ(R−P)\delta (R – P)δ(R−P) \)が減少し、
裏切りが再び最適解になってしまいます。
4. ゲームの終わりが近づいたとき
途中で有限回ゲームになった、つまり関係の「最終回」が見えた瞬間、
未来の価値が消失し、実質 δ = 0 になります。
裏切りへの制裁
繰り返しゲームにおいて協力が維持されるためには、
裏切りが単なる誘惑に終わらず、明確なコスト(罰)を伴うことが重要です。
裏切りに対する制裁は、未来の利得を重視する割引率 \(δ\) の効果を強化し、
協力を持続させるための重要な仕組みとなります。
以下に有名な戦略の例を挙げます。
1. しっぺ返し(Tit-for-Tat)
最も有名な制裁戦略が Tit-for-Tat です。
- 相手が協力 → 自分も協力
- 相手が裏切り → 次のラウンドで一度だけ報復
この単純な仕組みによって、
裏切りに対して 確実にコストを課しつつ、恨みを長引かせない バランスが取れています。
Tit-for-Tat は
「優しい・仕返しする・寛容・読みやすい」
という4つの性質を持ち、繰り返しゲームで非常に強力です。
2. 厳格な制裁(Grim Trigger)
もう一つの代表的戦略が Grim Trigger(厳罰戦略)です。
- 相手が一度でも裏切る
以後ずっと裏切り続ける(協力は永遠に終了)
この戦略は制裁が重いため、
裏切りを絶対に許さない社会的規範や長期契約をモデル化するのに適します。
ただし、誤解があっても協力が全て破綻するため、
ノイズの多い環境では不安定になりがちです。(実社会とか)
どの制裁戦略にも共通する本質はシンプルです。
裏切った瞬間に得られる短期利益(T − R)を、未来の損失によって相殺すること。
制裁があることで、裏切りによって一時的に利得を得ても、
次回以降の協力が失われるため長期的に損をします。
これが協力の安定条件を作り出すわけです。
制裁は人間社会・動物社会にも普遍的に存在します。
- コウモリ: 血液をくれなかった個体には返報しない
- 人間社会: 裏切り者には社会的制裁(評判・信頼の喪失)
- オンラインゲーム: 協力しないプレイヤーがキックされる
こうした「評判と制裁」の仕組みは、
いずれも裏切りの短期利益を抑制する働きを持ちます。
協力は自然に生まれるものではなく、裏切りに対する制裁があることで、はじめて安定します。
おわりに
悲しいことに現代社会ではこの「未来への期待」すなわち割引率\(δ\)が構造的に低下しやすくなっています。
インターネットや SNS では匿名性と流動性が非常に高く、
相手と再び会う確率が低いため、やり取りは“一期一会”、つまり 一回ゲーム化 が進んでいます。
見知らぬ相手に侮蔑的な言葉を浴びせてしまう行動などは、
その関係に未来が存在しない(=δが極端に低い)状態の典型例 だと考えられます。
もちろん、単に他者との距離感を適切に取れない人が増えているという側面もあるでしょうが、
構造的に「裏切りのコストが限りなく低い環境」が整ってしまったことも事実です。
その一方で、強烈な誘引ワードや物語によって割引率を意図的に引き上げ、
“ここに属せばメリットがある”という未来価値を作り出せるコミュニティ──
いわゆるインフルエンサーや強力なブランドは、現代では非常に「強い」存在と言えるでしょう。
このように、現代社会で起きている多くの現象は、
ゲーム理論を通して一定程度分解し、理解することができます。
この複雑な世の中を生き抜くためにも、
日常のあらゆる場面に、ほんの少しゲーム理論の視点を取り入れてみるのも良いかもしれません。